Основные уравнения теории предельного равновесия. Основные уравнения теории предельного равновесия в общем случае напряженного состояния

22.05.2022

Энциклопедичный YouTube

1 / 5

Внутренние усилия возникают между частицами сплошного деформируемого тела в качестве реакции на прикладываемые внешние силы: поверхностные и объёмные . Эта реакция согласуется со вторым законом Ньютона , приложенным к частицам материальных объектов. Величина интенсивности этих внутренних сил называется механическим напряжением . Т.к. тело считается сплошным, эти внутренние силы распределяются непрерывно по всему объёму рассматриваемого объекта.

cos 2 ⁡ θ = 1 + cos ⁡ 2 θ 2 , sin 2 ⁡ θ = 1 − cos ⁡ 2 θ 2 , sin ⁡ 2 θ = 2 sin ⁡ θ cos ⁡ θ {\displaystyle \cos ^{2}\theta ={\frac {1+\cos 2\theta }{2}},\qquad \sin ^{2}\theta ={\frac {1-\cos 2\theta }{2}}\qquad {\text{,}}\qquad \sin 2\theta =2\sin \theta \cos \theta }

Тогда можно получить

σ n = 1 2 (σ x + σ y) + 1 2 (σ x − σ y) cos ⁡ 2 θ + τ x y sin ⁡ 2 θ {\displaystyle \sigma _{\mathrm {n} }={\frac {1}{2}}(\sigma _{x}+\sigma _{y})+{\frac {1}{2}}(\sigma _{x}-\sigma _{y})\cos 2\theta +\tau _{xy}\sin 2\theta }

Касательное напряжение также действует на площадке площадью d A {\displaystyle dA} . Из равенства проекций сил на ось τ n {\displaystyle \tau _{\mathrm {n} }} (ось y ′ {\displaystyle y"} ) получаем:

∑ F y ′ = τ n d A + σ x d A cos ⁡ θ sin ⁡ θ − σ y d A sin ⁡ θ cos ⁡ θ − τ x y d A cos 2 ⁡ θ + τ x y d A sin 2 ⁡ θ = 0 τ n = − (σ x − σ y) sin ⁡ θ cos ⁡ θ + τ x y (cos 2 ⁡ θ − sin 2 ⁡ θ) {\displaystyle \ {\begin{aligned}\sum F_{y"}&=\tau _{\mathrm {n} }dA+\sigma _{x}dA\cos \theta \sin \theta -\sigma _{y}dA\sin \theta \cos \theta -\tau _{xy}dA\cos ^{2}\theta +\tau _{xy}dA\sin ^{2}\theta =0\\\tau _{\mathrm {n} }&=-(\sigma _{x}-\sigma _{y})\sin \theta \cos \theta +\tau _{xy}\left(\cos ^{2}\theta -\sin ^{2}\theta \right)\\\end{aligned}}}

Известно, что

cos 2 ⁡ θ − sin 2 ⁡ θ = cos ⁡ 2 θ , sin ⁡ 2 θ = 2 sin ⁡ θ cos ⁡ θ {\displaystyle \cos ^{2}\theta -\sin ^{2}\theta =\cos 2\theta \qquad {\text{,}}\qquad \sin 2\theta =2\sin \theta \cos \theta }

Тогда можно получить

τ n = − 1 2 (σ x − σ y) sin ⁡ 2 θ + τ x y cos ⁡ 2 θ {\displaystyle \tau _{\mathrm {n} }=-{\frac {1}{2}}(\sigma _{x}-\sigma _{y})\sin 2\theta +\tau _{xy}\cos 2\theta }

Обратная задача.

Прямая задача

Построение кругов Мора

Графический метод исследования напряженного состояния в точке.

Можно оказать, что уравнения , представляют уравнение окружности в параметрической форме. Поэтому для графического метода исследования напряженного состояния используются круги напряжений, называемые кругами Мора.

В теории напряженного состояния можно разграничить две основные задачи:

Прямая задача: в точке известны положение главных площадок и соответствующие им главные напряжения, требуется определить нормальные и касательные напряжения по площадкам, наклоненным к главным под углом a.

Обратная задача: в точке известны нормальные и касательные напряжения, действующие по двум взаимно перпендикулярным площадкам, проходящим через данную точку, требуется определить главные напряжения и положение главных площадок.

Рассмотрим решение этих задач графическим методом

Аналитическое решение прямой задачи определяется формулами (4.6) – (4.9).

Для графического решения строится на плоскости в координатах s-t круг Мора

(рис. 4.9) в следующей последовательности.

Рис. 4.9

Выбирается прямоугольная система координат так, чтобы ось абсцисс была параллельна большему из главных напряжений s 1 , по этой оси в выбранном масштабе откладывются отрезки ОА и ОВ, численно равные напряжениям s 1 и s 2 , а на их разности (на отрезке АВ) как на диаметре проводим окружность с центром в точке С.

Из крайней левой точки (В) круга проводим луч, параллельный внешней нормали к рассматриваемой площадке, т.е. под углом a к оси s. Точка пересечения этого луча с окружностью (D a) имеет своими координатами отрезки D a K a и OK a , численно равные касательному t a и нормальному s a напряжениям, действующим на рассматриваемой площадке.

СК α =СК β =СD α cos2α =cos2α

Точка D b , лежащая на противоположном конце диаметра от точки D a , характеризует напряжения s β и t b , действующие по наклонной площадке, перпендикулярной к первой.

Выполненные преобразования проведены с учетом, что 1+cos2α = 2cos 2 α., 1-cos2α = 2sin 2 α.

Полученные выражения для s a , s b , τ α и τ β полностью совпадают с аналитическими формулами (4.6) - (4.9).

В заключение следует отметить, что каждая точка круга Мора имеет своими координатами напряжения, действующие на соответствующей площадке, следовательно, зная главные напряжения для плоского напряженного состояния, можно с помощью круга Мора определить напряжения, действующие на различных площадках, проходящих через данную точку. Максимальное касательное напряжение соответствует точке D c и равно радиусу круга.

Довольно часто приходится решать обратную задачу, т. е. по напряжениям на произвольных площадках s a , t a , s b , t b определять величину и направление главных напряжений. Проще эта задача решается графически, т. е. с помощью круга Мора (рис. 4.10). Рассмотрим порядок его построения.

Прямоугольную систему координат s, t выберем так, чтобы ось абсцисс была параллельна большему из нормальных напряжений (пусть s a >

параллельна большему из нормальных напряжений (пусть s a > s b). На оси s отложим в выбранном масштабе отрезки ОК a , ОК b , численно равные s a и s b . Из точек К a и К b проведем перпендикуляры К a D a , К b D b , которые численно равны соответственноt a и τ β (К a D a = t a , К b D b = τ β = - t a). На отрезке D a D b , как на диаметре, построим круг с центром в точке С. Крайнюю правую точку пересечения круга с осью s обозначим буквой А, крайнюю левую – буквой В. Касательные напряжения в этих точках равны нулю, следовательно, ОА=s 1 , ОВ=s 2 – главные напряжения (.в соответствии с прямой задачей).

Из рис.6.10 определим радиус круга R и величину отрезка ОС (4.12)

C учетом выражений (4.12) , (4.13) получим следующие формулы для главных напряжений

ОА= σ I = ОС + R = + (4.14)

ОВ = σ II = ОС – R = - (4.15)

Для определения направления главного напряжения s 1 проведем луч через крайнюю левую точку круга В и точку D a ¢, которая симметрична точке D a относительно оси s. Направление луча ВD a ¢ совпадает с направлением s 1 , направление s 2 перпендикулярно ему. Угол a 0 определится из треугольника ВК a D a ¢ (рис. 6.10):

Угол a 0 считается положительным, если его откладывают от оси s против часовой стрелки.

В элементарном параллелепипеде, по граням которого действуют все три главных напряжения, рассмотрим произвольную площадку a, нормаль к которой составляет с координатными осями 1,2,3 углы α 1 α 2 α 3 .(рис. 4. 11). На этой площадке будет действовать полное напряжение р α , составляющее с нормалью n угол α. Определим его проекции на нормаль к площадке - σ α и на саму площадку – τ α .

Рис.4.11

Нормальное напряжение, исполь-зуя принцип суперпозиции, можно пред-ставить выражением =,

где- напряжение на рассматриваемой площадке, вызванное действием , а ,- соответственно от напряжений и.Для вычисления этих величин воспользуемся формулой для линейного напряжённого состояния: =, =, =.

С учетом этих значений нормальные напряжения на произвольной площадке определятся равенством

Для вывода формулы касательных напряжений τ α следует рассмотреть его векторную величину . Так как , то .

Опуская выводы, которые следуют из уравнений равновесия рассматриваемой трёх- гранной пирамиды (рис. 3.11), запишем формулу в окончательном виде для вектора полного напряжения на площадке n α:

С учётом этого выражения

В качестве примера рассмотрим напряжения на площадке, равнонаклонённой ко всем главным площадкам. Такая площадка называется октаэдрической, а напряжения, действующие на этой площадке, называются октаэдрическими.

Так как для такой площадки , а учитывая, что всегда

То . Следовательно (4.20)

Так же, как и в случае плоского напряженного состояния, при объемном напряженном состоянии сумма нормальных напряжений по трем взаимно перпендикулярным площадкам, проходящим через рассматриваемую точку, есть величина постоянная.

Рассмотрим графический метод анализа напряженного состояния в точке при объемном напряженном состоянии.

Прежде всего определим напряжения на площадках, параллельных одному из главных напряжений (рис. 4.12)

s 2

Круг Мора, соответствующий этому случаю, представлен на рис. 4.13 кругом «а».

Напряжения в семействе площадок, параллельных s 2 , определяются по кругу «б», а в семействе площадок, параллельных s 3 – с помощью круга «в».

В теории упругости доказывается, что площадкам общего положения соответствуют точки, лежащие в заштрихованной области (рис. 4.13).

Из представленного рисунка следует, что наименьшее и наибольшее нормальные напряжения равны наименьшему и наибольшему главным напряжениям , .

Наибольшие касательные напряжения равны радиусу наибольшего круга

и действуют по площадке, равнонаклонённой к площадкам максимального и минимального из главных напряжений ().

Круги мора - круговые диаграммы, дающие наглядное представление о напряжениях в разных сечениях, проходящих через данную точку. В системе координат τ n - σ n - три (полу)окружности, которых по оси абсцисс являются разностью главных нормальных напряжений σ 1 , σ 2 , σ 3 (рис.). Максимальная окружность радиусом (σ 1 -σ 3)/2 охватывает две внутренние окружности радиусами (σ 1 -σ 2)/2 и (σ 2 -σ 3)/2, касающихся в точке σ 2 . Координаты точек в пространстве между дугами этих окружностей - нормальные и касательные в произвольно ориентированных площадках. На осях окружностей находятся соответственно . Положение точки σ 2 определяется коэффициентом Лоде - Надаи. Аналогично кругам Мора в координатах γ - ε строят для исследования деформированного состояния, где R 1 = (ε 2 -ε 1)/2 = 0,5γ 23 , R 2 = (ε 1 -ε 3)/2 = 0,5γ 31 , R 3 = (ε 1 -ε 2)/2 = 0,5γ 12

Круги Мора (круговая напряжений)

Энциклопедический словарь по металлургии. - М.: Интермет Инжиниринг . Главный редактор Н.П. Лякишев . 2000 .

Смотреть что такое "Круги мора" в других словарях:

круги Мора - Круговые диаграммы, дающие наглядное представление о напряжениях в разных сечениях, проходящих через данную точку. В системе координат тл—ал — три (полу)окружности, диам. к рых по оси абсцисс являются разностью главных нормальных… … Справочник технического переводчика

Круги - Круги: Содержание 1 Населённые пункты 1.1 Белоруссия 1.2 Россия 1.3 Украина … Википедия

Круги (значения) - Населённые пункты: Круги (укр. Круги) село, входит в Вышгородский район Киевской области Украины. Круги (укр. Круги) село на Украине, находится в Тывровском районе Винницкой области. Круги (белор. Кругі) деревня в… … Википедия

ВЕЛИКОБРИТАНИЯ - (Great Britain) гос во в Зап. Европе, расположено на Британских о вах. Офиц. назв. В. Соединенное Королевство Великобритании и Северной Ирландии (United Kingdom of Great Britain and Northern Ireland); часто всю В. неточно именуют Англией (по назв … Советская историческая энциклопедия

Великобритания - I Великобритания (Great Britain) остров в Атлантическом океане, входящий в группу Британских островов (См. Британские острова). См. Великобритания (государство). II Великобритания (Great Britain) официальное название Соединённое… …

Великобритания (государство) - Великобритания (Great Britain); официальное название ‒ Соединённое Королевство Великобритании и Северной Ирландии (The United Kingdom of Great Britain and Northern Ireland). I. Общие сведения В. ‒ островное государство на С. З. Европы; занимает… … Большая советская энциклопедия

Франция - (France) Французская Республика (République Française). I. Общие сведения Ф. государство в Западной Европе. На С. территория Ф. омывается Северным морем, проливами Па де Кале и Ла Манш, на З. Бискайским заливом… … Большая советская энциклопедия

Коммунизм - Словом К. обозначают: во первых, такой общественный порядок, при котором в сфере имущественных отношений отсутствует частная собственность (всякая или только на недвижимость), а в сфере отношений семейных место брака занимает беспорядочное… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

История коммунистических учений - Коммунизм общее название учений, провозглашающих целью отмену частной собственности и освобождение человека и общества от экономического и социального гнета. Слово «коммунизм» объединяет те религиозные, нравственные и экономические учения,… … Википедия

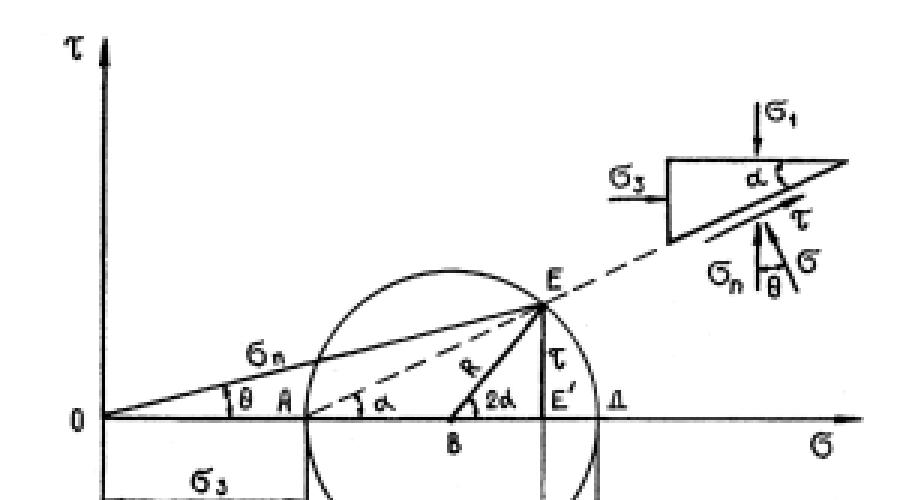
Круг Мора (рис. 8.2 ) вычерчивается в прямоугольной системе координат. Полагается, что σ 1 ≥σ 2

Рис. 8.2. Графическое представление напряженного состояния грунта (круг Мора)

Построение круга Мора производится в следующей последовательности. От начала координат откладываем значения σ 1 и σ 3 . Из точки В проводят окружность радиусомт R . Любая точка E на окружности характеризует напряженное состояние грунта в плоскости, проходящей через рассматриваемую точку. Угол наклона α линии ЕА - это угол наклона рассматриваемой площадки к главной. Центральный угол наклона отрезка EB равен 2α. Нормальные напряжения по этой площадке а представляются по горизонтальной оси отрезком ОЕ", касательные τ - перпендикулярным отрезком ЕЕ" .

Значения σ и τ могут быть определены через σ 1 и σ 3 по формулам (8.1) и (8.2).

Максимальные и минимальные касательные напряжения соответствуют sin 2α = 1 и sin 2α = -1, т.е. углам 2α=π/2 или 3π/2 (α=45° или 135°).

Полное результирующее напряжение на рассматриваемой площадке

Угол отклонения σ n от нормали к площадке

(8.4)

Значение угла θ при изменении угла α от 0 до 90° сначала возрастает от нуля до некоторого θ max , а затем убывает до нуля.

Угол θ максимален, когда линия ОE станет касательной к кругу напряжений. Из треугольника ОBЕ :

(8.5)

Максимальное отклонение полного (результирующего) напряжения на угол θmax нормали к площадке имеет место при:

Следовательно, отклонения площадки скольжения от направления наибольшего главного напряжения σ 1

(8.7)

Таким образом, в предельном состоянии в каждой точке грунта имеются две сопряженные площадки скольжения, наклоненные под углом 45°- φ/2 к линии действия максимального и 45° + φ/2 - минимального главного напряжения (рис. 8.3 ).

Рис. 8.3. Ориентация площадок скольжения относительно главных напряжений: 1, 2 - площадки скольжения

Для сыпучих грунтов во всех случаях θ max не может быть больше угла внутреннего трения φ. А разрушение сыпучих грунтов наступает, когда угол отклонения полного(результирующего) напряжения равен углу внутреннего трения:

θ max = φ (8.8)

Выражение (8.8) является условием прочности грунта. Тогда уравнение предельного равновесия можно записать в следующем виде:

(8.9)

Выражение (8.9) известно в механике грунтов как условие прочности (предельного равновесия) для песчаных (сыпучих) грунтов. После несложных тригонометрических преобразований это выражение можно записать в следующем виде:

(8.10)

(8.11)

Это выражение часто используют в теории давления грунтов на ограждения (глава 10). Для связных грунтов также можно записать условие предельного равновесия, предварительно построив круги Мора (рис. 8.4 ) по результатам испытания в стабилометре (см. рис. 5.7).

Рис. 8.4. Круги Мора, построенные по результатам испытания образцов грунта на сжатие в стабилометре

Радиус круга

ВД = (σ 1 - σ 3)/2 (8.12)

а отрезок О"Д можно найти из выражения

Отрезок О"О , отсекаемый наклонной линией на оси абсцисс (см. рис. 8.4), называют давлением связности, которое можно представить в виде

(8.14)

Давление связности (8.14) можно условно считать начальным давлением связного грунта, которое необходимо преодолеть при испытании на сдвиг. Зная ВД (8.12) и О"Д (8.13), а также используя (8.14), найдем

(8.15)

Выражение (8.15), связывающее главные напряжения в момент разрушения образца с углом внутреннего трения, принято называть уравнением предельного равновесия для связных грунтов.

Уравнение (8.15) в некоторых случаях удобно использовать не в главных напряжениях, а в компонентах, записанных относительно координатных осей. Из сопротивления материалов известно, что:

(8.16)

Тогда, рассматривая совместно уравнения (8.15) и (8.16), можно записать уравнение предельного равновесия в следующем виде:

(8.17)

Аналогичным образом можно выразить и уравнение (8.9).

Круговые диаграммы, дающие наглядное представление о напряжениях в разных сечениях, проходящих через данную точку. В системе координат τ n - σ n - три (полу)окружности, диаметр которых по оси абсцисс являются разностью главных нормальных напряжений σ 1 , σ 2 , σ 3 (рис.). Максимальная окружность радиусом (σ 1 -σ 3)/2 охватывает две внутренние окружности радиусами (σ 1 -σ 2)/2 и (σ 2 -σ 3)/2, касающихся в точке σ 2 . Координаты точек в пространстве между дугами этих окружностей - нормальные и касательные напряжения в произвольно ориентированных площадках. На осях окружностей находятся соответственно главные напряжения. Положение точки σ 2 определяется коэффициентом Лоде - Надаи. Аналогично кругам Мора в координатах γ - ε строят для исследования деформированного состояния, где R 1 = (ε 2 -ε 1)/2 = 0,5γ 23 , R 2 = (ε 1 -ε 3)/2 = 0,5γ 31 , R 3 = (ε 1 -ε 2)/2 = 0,5γ 12

Круги Мора (круговая диаграмма напряжений)

- МОРА, или протос хронос - единица отсчета времени в стихе у античных теоретиков метрики...
Литературная энциклопедия
- МОРА - у римлян, хронос протос у греков, матра у индусов - есть означение времени, потребного для того, чтобы пропеть краткий слог. Это была первичная единица квантитативного стиха, так сказать его атом....
Словарь литературных терминов
- МО´РА - в древнелатинской метрике самое краткое время, необходимое для произнесения простого слога, состоящего из гласного звука или согласного с гласной...
Поэтический словарь
- вид гидростатич. весов, рычажные весы с неравноплечным коромыслом для измерения плотности жидкостей и тв. тел методом гидростатического взвешивания. Сконструированы К. Ф. Мором в 1847...
Естествознание. Энциклопедический словарь
- Хосе Мария Луис - мекс. политич. деятель, экономист и историк. Теолог и юрист по образованию, М. в 20-е гг. 19 в. занимался педагогич. и журналистской деятельностью...
Советская историческая энциклопедия
- см. Мора зажим...
Большой медицинский словарь
- самостоятельный отряд спартанской пехоты, в которой всех М. было 6. Каждая М. делилась на 2 лоха, каждый лох по 4 пентекостии, в свою очередь состоявшие из 2 эномотий...
Энциклопедический словарь Брокгауза и Евфрона
- или хронос протос, в античном стихосложении нормальная продолжительность произнесения краткого слога, самая малая единица счёта времени в стихе...
- Мануэль, деятель коммунистического движения Коста-Рики. Родился в рабочей семье. По профессии адвокат. В 1920-30-е гг. руководил демократическим молодёжным и студенческим движением страны...
Большая Советская энциклопедия
- рычажные весы с неравноплечным коромыслом, предназначенные для определения плотности жидкостей и твёрдых тел методом гидростатического взвешивания...
Большая Советская энциклопедия
- В фонологии древнегреческого, японского, санскрита, латинского выделяют мору − ритмическую единицу, равную открытому слогу с краткой гласной...
Грамматологический словарь
- м"...
Русский орфографический словарь
- См....
Пятиязычный словарь лингвистических терминов
- муж., вологод. момра, мрак, тьма, морок, сумрак, потемки...
Толковый словарь Даля
- Ядрёна мора! Пск. Бран. Восклицание, выражающее раздражение, негодование. СПП 2001, 53...
Большой словарь русских поговорок
- 1) отряды спартанской пехоты в 400 чел. 2) итальянская...
Словарь иностранных слов русского языка

"Круги мора" в книгах

О СТИЛЕ ЙОКАИ МОРА

Из книги История человеческой глупости автора Рат-Вег Иштван

О СТИЛЕ ЙОКАИ МОРА В "Немзети уйшаг" за 1846 год на 254-й странице в статье театрального критика можно прочитать:"Даже дважды наново переиначенная народная драма некоего Мора Йокаи "Два опекуна" умерла неоплаканной на сцене Национального театра… Господи, прости родителю

Спасение от мора

Из книги Мифы и предания Древнего Рима автора Лазарчук Дина Андреевна

Спасение от мора На восьмом году царствования Нумы Помпилия в Рим пришла страшная моровая болезнь, терзавшая к тому времени всю Италию. Страх охватил жителей города, и тогда Риму явилось божественное знамение. Говорят, что прямо в руки царю с неба опустился медный щит. По

Бітва за Варажскае мора

Из книги ДзесяцЬ Бітвау автора Чарняўскі Міхась

Мара (маруха, мора)

Из книги Славянские боги, духи, герои былин автора Крючкова Ольга Евгеньевна

Мара (маруха, мора)

Из книги Славянские боги, духи, герои былин. Иллюстрированная энциклопедия автора Крючкова Ольга Евгеньевна

Мара (маруха, мора) Мара (маруха, мора) – в славянской мифологии злой дух в образе женщины, сначала считавшийся воплощением смерти и мора, но позже так стали называть всех злых и вредоносных духов.У северных славян считалось, что мара мрачное и злое привидение, которое днём

Мора весы

Из книги Большая энциклопедия техники автора Коллектив авторов

Мора весы Мора весы – прибор, относящийся к виду гидростатических весов, представляющий собой рычажные весы, оснащенные неравноплечным коромыслом. Разработаны весы в 1847 г. немецким химиком К. Ф. Мором.При помощи весов Мора осуществляются измерение и определение

Мара, маруха, мора

Из книги Мифологический словарь автора Арчер Вадим

Мара, маруха, мора (слав.) - злой дух, первоначально - воплощение смерти, мора, позднее так стали называть любых вредоносных духов. М. приписывалась способность к оборотничеству. Мара - имя чучела, сжигаемого на костре в ночь на Ивана

Мора

БСЭ

Мора Вальверде Мануэль

Из книги Большая Советская Энциклопедия (МО) автора БСЭ

Мора весы

Из книги Большая Советская Энциклопедия (МО) автора БСЭ

47. Политические воззрения Т. Мора

Из книги История политических и правовых учений. Шпаргалки автора Князева Светлана Александровна

47. Политические воззрения Т. Мора Томас Мор (1478–1535), правовед по образованию, прославился как блестящий адвокат, был избран в парламент, затем занимал должность судьи, помощника шерифа г. Лондона и другие должности. В 1516 г. он опубликовал «Золотую книгу, столь же полезную,

18 УТОПИЗМ Т. МОРА И Т. КАМПАНЕЛЛЫ

Из книги История политических и правовых учений [Шпаргалка] автора Баталина В В

18 УТОПИЗМ Т. МОРА И Т. КАМПАНЕЛЛЫ Томас Мор (1478–1535) – английский юрист, философ, политический деятель. Главное произведение: «Весьма полезная, а также и занимательная, поистине золотая книжица о наилучшем устройстве государства и о новом острове Утопия». Отсюда появление

17. Утопизм Т. Мора и Т. Кампанеллы

Из книги История правовых и политических учений. Шпаргалка автора Шумаева Ольга Леонидовна

17. Утопизм Т. Мора и Т. Кампанеллы Томас Мор (1478–1535 гг.) – писатель социалистического направления, основным трудом которого является «Утопия» (1516 г.).Общество, согласно Т. Мору, является результатом заговора богачей. Государство же – их простое орудие. Они используют его в

Поэзия Томаса Мора

Из книги Поэзия Томаса Мора автора Шульц Юрий Францевич

Поэзия Томаса Мора – Thomas More Epigrammata. The history of king Richard III Томас Мор Эпиграммы. История Ричарда III «Литературные памятники». М., «Наука», 1973 Издание подготовили: М. Л. Гаспаров, Е. В. Кузнецов, И. Н. Осиновский, Ю. Ф. Шульц Бычков М.Н. mailto:[email protected]– Великий английский гуманист, философ и

Мора

Из книги Хелависа и группа «Мельница». Не только песни [сборник] автора О`Шей Наталья Хелависа

Мора Текст: Елена Косачева (припев из народной песни) Летят кони Стрибога - ветер в гриву, Перуна подкова - пропасть под молнией, Кони Даждьбога дождем резвятся, И конь коней - корона на небе. Жаркой волной - в глаза жрице, Железом каленым - жрице к запястьям, Звездами

Основные уравнения теории предельного равновесия. Основные уравнения теории предельного равновесия в общем случае напряженного состояния

Читайте также

Энциклопедичный YouTube

Смотреть что такое "Круги мора" в других словарях:

"Круги мора" в книгах

О СТИЛЕ ЙОКАИ МОРА

Спасение от мора

Бітва за Варажскае мора

Мара (маруха, мора)

Мара (маруха, мора)

Мора весы

Мара, маруха, мора

Мора

Мора Вальверде Мануэль

Мора весы

47. Политические воззрения Т. Мора

18 УТОПИЗМ Т. МОРА И Т. КАМПАНЕЛЛЫ

17. Утопизм Т. Мора и Т. Кампанеллы

Поэзия Томаса Мора

Мора