Istražite kontinuitet funkcije dvije varijable. Granica i kontinuitet funkcije dvije varijable. Granica funkcije od nekoliko varijabli
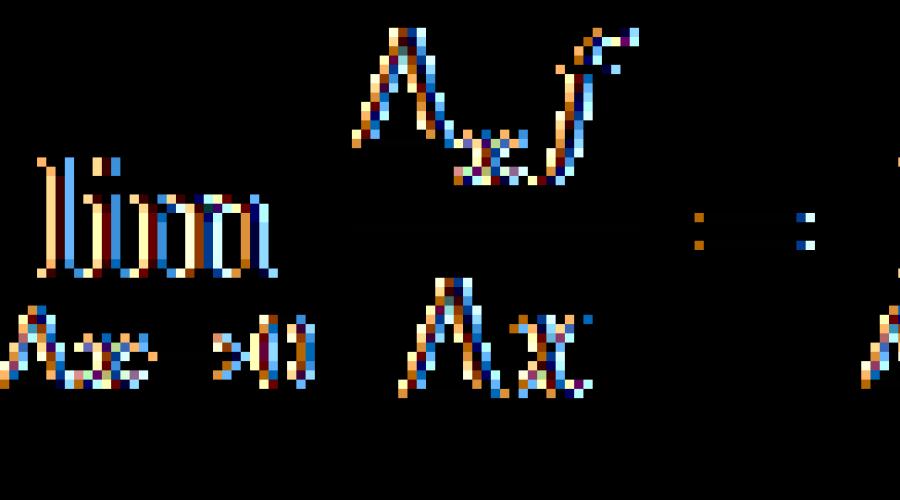
Pročitajte također
Dokažimo na primjer (7).
Neka bude ( x k, y k) → (X 0 , at 0) ((x k, y k) ≠ (X 0 , at 0)); onda
(9)Dakle, granica na lijevoj strani (9) postoji i jednaka je desnoj strani (9), a budući da je niz ( x k, y k) teži ( X 0 , at 0) prema bilo kojem zakonu, ta granica je jednaka granici funkcije f (x, y) ∙φ (x, y) u tački ( X 0 , at 0).
Teorema. if funkcija f (x, y) ima granicu različitu od nule u tački ( X 0 , at 0), tj.
onda postoji δ > 0 tako da za sve X, at
< δ, (10)zadovoljava nejednakost
(12)Stoga, za takve (x, y)
one. vrijedi nejednakost (11). Iz nejednakosti (12) za navedeno (x, y) trebalo bi
odakle na A> 0 iA< 0 (сохранение знака).
Po definiciji, funkcija f(x) = f (x 1 , …, x n) = A ima ograničenje u tački
, jednako broju ALI, označen na sljedeći način:(oni pišu više f(x) → A (x → x 0)) ako je definiran u nekom susjedstvu tačke x 0 , osim možda za sebe, i ako postoji granica
šta god da je težnja x sekvenca od 0 poena Xk iz navedenog susjedstva ( k= 1, 2, ...) osim x 0 .
Druga ekvivalentna definicija je sljedeća: funkcija f ima u tački x 0 granica jednako ALI, ako je definiran u nekom susjedstvu tačke x 0 , osim možda za sebe, i za bilo koje ε > 0 postoji δ > 0 tako da
(13)za sve X zadovoljavanje nejednakosti
0 < |x – x 0 | < δ.
Ova definicija je zauzvrat ekvivalentna sljedećem: za bilo koje ε > 0 postoji susjedstvo U (x 0 ) bodova x 0 tako da za sve X
U(x 0 ) , X ≠ x 0 , nejednakost (13) je zadovoljena.Očigledno, ako je broj ALI postoji granica f(x) in x 0 , onda ALI postoji ograničenje funkcije f(x 0 + h) od h na nultoj tački:
i obrnuto.
Razmotrite neku funkciju f, dat u svim tačkama susjedstva tačke x 0, osim možda tačke x 0; neka je ω = (ω 1 , ..., ω P) je proizvoljan vektor dužine jedan (|ω| = 1) i t> 0 je skalar. View Points x 0 + tω (0 < t) formiraju odlazni x 0 zraka u smjeru vektora ω. Za svaki ω možemo razmotriti funkciju
(0 < t < δ ω)iz skalarne varijable t, gdje je δ ω broj koji ovisi o ω. Granica ove funkcije (od jedne varijable t)
ako postoji, prirodno je nazvati granicu f u tački x 0 u smjeru vektora ω.
Pisaće
ako je funkcija f definisano u nekom kraju x 0 , osim možda x 0 , i za bilo koje N> 0, postoji δ > 0 takvo da | f(x) | >N, čim 0< |x – x 0 | < δ.Možete pričati o limitu f, kada X → ∞:
(14)Na primjer, u slučaju konačnog broja ALI Jednakost (14) treba shvatiti u smislu da se za bilo koje ε > 0 može odrediti takva N> 0, što za bodove X, za koje | x| > N, funkcija f je definirana i nejednakost
.Dakle, granica funkcije f(x) = f(x 1 , ..., x n) od P varijable se definira analogno na isti način kao i za funkciju dvije varijable.
Dakle, prelazimo na definiciju granice funkcije nekoliko varijabli.
Broj ALI naziva se granica funkcije f(M) at M → M 0 ako za bilo koji broj ε > 0 uvijek postoji broj δ > 0 takav da za bilo koju tačku M, osim M 0 i zadovoljava uvjet | MM 0 | < δ, будет иметь место неравенство |f(M) – ALI | < ε.
Limit označava
U slučaju funkcije dvije varijableGranične teoreme. Ako funkcije f 1 (M) i f 2 (M) at M → M 0 svaki teži konačnoj granici, tada:
Primjer 1 Pronađite ograničenje funkcije:
Odluka. Granicu transformiramo na sljedeći način:
Neka bude y = kx, onda
Primjer 2 Pronađite ograničenje funkcije:
Odluka. Koristimo prvu izvanrednu granicu
OndaPrimjer 3 Pronađite ograničenje funkcije:
Odluka. Koristimo drugu izuzetnu granicu
OndaKontinuitet funkcije nekoliko varijabli
Po definiciji, funkcija f (x, y) je kontinuiran u tački ( X 0 , at 0) ako je definiran u nekom svom susjedstvu, uključujući i samu tačku ( X 0 , at 0) i ako je granica f (x, y) u toj tački jednaka je njegovoj vrijednosti u njemu:
(1)Uslov kontinuiteta tj. funkcija f je kontinuiran u tački ( X 0 , at 0) ako je funkcija kontinuirana f(X 0 + Δ X, at 0 + Δ y) na varijablama Δ X, Δ at na Δ X = Δ y= 0.
Možete unijeti inkrement Δ i funkcije i = f (x, y) u tački (x, y) što odgovara inkrementima Δ X, Δ at argumentima
Δ i = f(X + Δ X, at + Δ y) – f (x, y)
i na ovom jeziku definišu kontinuitet f in (x, y) : funkcija f kontinuirano u tački (x, y) , ako
(1"")Teorema. Zbir, razlika, proizvod i količnik kontinuiranog u tački ( X 0 , at 0) funkcije f i φ je kontinuirana funkcija u ovoj tački, osim, naravno, u slučaju parcijalnog φ ( X 0 , at 0) ≠ 0.
trajno sa može se posmatrati kao funkcija f (x, y) = sa iz varijabli x, y. On je kontinuiran u ovim varijablama jer
|f (x, y) – f (X 0 , at 0) | = |s - s| = 0 0.Funkcije su sljedeće po složenosti. f (x, y) = X i f (x, y) = at. One se također mogu smatrati funkcijama (x, y) , i oni su kontinuirani. Na primjer, funkcija f (x, y) = X odgovara svakom bodu (x, y) broj jednak X. Kontinuitet ove funkcije u proizvoljnoj tački (x, y) može se dokazati ovako.
Kontinuitet funkcije
Funkcija dvije varijable f (x, y), definirane u tački (x 0 , y 0) iu nekom njenom susjedstvu, naziva se kontinuiranom u tački (x 0 , y 0) ako je granica ove funkcije u tačka (x 0 , y 0 ) jednaka je vrijednosti ove funkcije f(x 0 , y 0), tj. ako
Funkcija koja je neprekidna u svakoj tački nekog regiona naziva se kontinuirana u tom regionu. Neprekidne funkcije dvije varijable imaju svojstva slična onima neprekidnih funkcija jedne varijable.
Ako u nekoj tački (x 0 , y 0) uslov kontinuiteta nije zadovoljen, onda kažemo da je funkcija f (x, y) u tački (x 0 , y 0) diskontinuirana.
Diferencijacija funkcije dvije varijable
Parcijalni derivati prvog reda
Još važnija karakteristika varijacije funkcije su granice:
granica omjera

naziva se parcijalni izvod prvog reda funkcije z = f (x, y) u odnosu na argument x (skraćeno kao parcijalni izvod) i označava se simbolima ili ili
Isto tako, granica

naziva se parcijalni izvod funkcije z = f (x, y) u odnosu na argument y i označava se simbolima ili ili.
Pronalaženje parcijalnih izvoda naziva se parcijalna diferencijacija.
Iz definicije parcijalnog izvoda, slijedi da kada se pronađe pomoću jednog određenog argumenta, drugi parcijalni argument se smatra konstantom. Nakon što se izvrši diferencijacija, oba parcijalna argumenta se ponovo smatraju varijablama. Drugim riječima, parcijalni derivati i su funkcije dvije varijable x i y.
Parcijalni diferencijali
Vrijednost
se zove glavni linearni dio prirasta? x f (linearno u odnosu na parcijalni inkrement argumenta?x). Ova vrijednost se naziva parcijalni diferencijal i označava se simbolom d x f.

Slično

Totalni diferencijal funkcije dvije varijable
Po definiciji, ukupni diferencijal funkcije dvije varijable, označen simbolom d f, je glavni linearni dio ukupnog priraštaja funkcije:
Pokazalo se da je ukupni diferencijal jednak zbiru parcijalnih diferencijala. Sada se formula za ukupni diferencijal može prepisati na sljedeći način:
Naglašavamo da se formula za ukupni diferencijal dobija pod pretpostavkom da su parcijalni derivati prvog reda

su kontinuirane u nekom susjedstvu tačke (x, y).
Funkcija koja ima totalni diferencijal u nekoj tački naziva se diferencijabilna u toj tački.
Da bi funkcija dvije varijable bila diferencibilna u jednoj tački, nije dovoljno da ima sve parcijalne derivate u toj tački. Neophodno je da sve ove parcijalne derivacije budu kontinuirane u nekoj okolini razmatrane tačke.
Derivati i diferencijali višeg reda
Razmotrimo funkciju dvije varijable z =f (x, y). Gore je već napomenuto da su parcijalni derivati prvog

su same funkcije dvije varijable i mogu se diferencirati s obzirom na x i y. Dobijamo derivate višeg (drugog) reda:
Već postoje četiri parcijalne derivacije drugog reda. Bez dokaza se daje tvrdnja: Ako su mješoviti parcijalni derivati drugog reda kontinuirani, onda su jednaki:

Razmotrimo sada diferencijal prvog reda
To je funkcija četiri argumenta: x, y, dx, dy, koji mogu poprimiti različite vrijednosti.
Diferencijal drugog reda se izračunava kao diferencijal diferencijala prvog reda: pod pretpostavkom da su diferencijali parcijalnih argumenata dx i dy konstante:

Mnoge pojave koje se javljaju u prirodi, ekonomiji, društvenom životu ne mogu se opisati pomoću funkcije jedne varijable. Na primjer, profitabilnost preduzeća zavisi od dobiti, fiksnog i obrtnog kapitala. Za proučavanje ove vrste zavisnosti uvodi se koncept funkcije nekoliko varijabli.
U ovom predavanju razmatraju se funkcije dvije varijable, jer se svi osnovni pojmovi i teoreme formulisani za funkcije dvije varijable mogu lako generalizirati na slučaj većeg broja varijabli.
Neka bude B je skup uređenih parova realnih brojeva .
Definicija 1 Ako je, prema nekom zakonu, svaki uređeni par brojeva povezan s jednim realnim brojem, onda kažemo da funkcija dvije varijable ili . Zovu se brojevi nezavisne varijable ili argumenti funkcije, a broj je zavisna varijabla.
Na primjer, formula koja izražava zapreminu cilindra je funkcija dvije varijable: - polumjera osnove i - visine.
Par brojeva se ponekad naziva tačka, a funkcija dve varijable ponekad se naziva funkcija tačke.
Vrijednost funkcije
na tački označavaju ![]() ili
i nazovi privatna vrijednost funkcije dvije varijable.
ili
i nazovi privatna vrijednost funkcije dvije varijable.
Skup svih tačaka u kojima je funkcija definirana , zove se domenu definicije ovu funkciju. Za funkciju od dvije varijable, domen definicije je cijela koordinatna ravan ili njen dio omeđen jednom ili više linija.
Na primjer, domen definicije funkcije je cijela ravan i funkcije ![]() je jedinična kružnica sa središtem na početku (
je jedinična kružnica sa središtem na početku ( ![]() ili .
ili .
Koncepti ograničenja i kontinuiteta funkcije dvije varijable analogni su slučaju jedne varijable.
Neka je proizvoljna tačka ravni. - susjedstvo tačke naziva se skup svih tačaka čije koordinate zadovoljavaju nejednakost . Drugim riječima, - susjedstvo tačke su sve unutrašnje tačke kružnice sa centrom u tački i radijusom .
Definicija 2 Broj je pozvan ograničenje funkcije at ![]() (ili u točki ) ako za bilo koji proizvoljno mali pozitivan broj postoji (ovisno o ) takav da za sve
(ili u točki ) ako za bilo koji proizvoljno mali pozitivan broj postoji (ovisno o ) takav da za sve ![]() zadovoljavanje nejednakosti , nejednakosti
zadovoljavanje nejednakosti , nejednakosti ![]() .
.
Granica je definirana na sljedeći način: ![]() ili
ili ![]() .
.
Primjer 1 Pronađite granicu  .
.
Odluka. Uvodimo notaciju ![]() , gdje . At
, gdje . At ![]() imamo to. Onda
imamo to. Onda
 .
.
Definicija 3 Funkcija se poziva kontinuirano u jednoj tački, ako je: 1) definisan u tački i njenoj okolini; 2) ima konačnu granicu; 3) ova granica je jednaka vrijednosti funkcije u tački , tj. ![]() .
.
Funkcija pozvao kontinuirano u nekom području, ako je kontinuirano u svakoj tački ovog područja.
Pozivaju se tačke u kojima uslov kontinuiteta nije zadovoljen prelomne tačke ovu funkciju. U nekim funkcijama tačke prekida formiraju čitave linije prekida. Na primjer, funkcija ima dvije linije prekida: axis() i axis().
Primjer 2 Pronađite tačke prekida funkcije  .
.
Odluka. Ova funkcija nije definisana u onim tačkama u kojima imenilac nestaje, odnosno u tačkama gde ![]() ili . To je kružnica sa središtem u početku i poluprečnika . To znači da će linija diskontinuiteta originalne funkcije biti kružnica.
ili . To je kružnica sa središtem u početku i poluprečnika . To znači da će linija diskontinuiteta originalne funkcije biti kružnica.
2 Parcijalni derivati prvog reda. puni diferencijal.
Parcijalni derivati višeg reda
Neka je data funkcija dvije varijable . Povećajmo argument i ostavimo argument nepromijenjen. Tada će funkcija dobiti pozvani inkrement djelomično povećanje promjenljivom i označeno je:
Slično, fiksiranjem argumenta i povećanjem argumenta, dobijamo privatni prirast funkcije preko varijable:
Vrijednost se poziva puno povećanje funkcije u tački .
Definicija 4 Parcijalni izvod funkcije dvije varijable jedna od ovih varijabli je granica omjera odgovarajućeg parcijalnog prirasta funkcije i priraštaja date varijable kada potonja teži nuli (ako ova granica postoji).
Parcijalni derivat se označava kao: ili, ili ![]() .
.
Dakle, po definiciji 4 imamo:
Parcijalne derivacijske funkcije izračunavaju se prema istim pravilima i formulama kao funkcija jedne varijable, uzimajući u obzir da pri diferenciranju u odnosu na varijablu , smatra se konstantnim, a kada se diferencira u odnosu na varijablu smatra se konstantnim.
Primjer 3 Pronađite parcijalne izvode funkcija:
Odluka:
1 Da biste pronašli, razmislite konstantan i diferenciran kao funkcija jedne varijable:
Slično, uz pretpostavku konstantne vrijednosti, nalazimo:
![]() .
.
 .
.
Definicija 5 Totalni diferencijal funkcije je zbir proizvoda parcijalnih izvoda ove funkcije i prirasta odgovarajućih nezavisnih varijabli, tj.
![]() .
.
Sa nepopravljenim: ![]() , a formula za ukupni diferencijal se može napisati kao
, a formula za ukupni diferencijal se može napisati kao
![]() ili
ili  .
.
Primjer 4 Pronađite puni diferencijal funkcije ![]() .
.
Odluka. As  , zatim po formuli ukupnog diferencijala nalazimo
, zatim po formuli ukupnog diferencijala nalazimo
 .
.
Parcijalni derivati se također nazivaju parcijalnim derivatima prvog reda.
Definicija 6 Parcijalni derivati drugog reda funkcije se nazivaju parcijalnim derivatima parcijalnih izvoda prvog reda.
Postoje četiri parcijalne derivacije drugog reda. Oni su označeni kako slijedi:
Or  ; ili
; ili  ;
;
Or  ; ili
; ili  .
.
Slično su definisane parcijalne derivacije 3., 4. i višeg reda. Na primjer, za funkciju imamo:
 ;
;  itd.
itd.
Drugi ili viši parcijalni derivati uzeti u odnosu na različite varijable se nazivaju mješoviti parcijalni derivati. Za funkciju to su derivati. Imajte na umu da u slučaju kada su mješovite derivacije kontinuirane, tada se ostvaruje jednakost.
Primjer 5 Pronađite parcijalne izvode drugog reda funkcije .
Odluka. Parcijalni derivati prvog reda za ovu funkciju nalaze se u primjeru 3:
Diferenciranje i s obzirom na varijable X i y, dobijamo:
3 Ekstremum funkcije nekoliko varijabli.
Neophodni i dovoljni uslovi za postojanje ekstremuma
Definicija 7 Tačka se zove minimalna (maksimalna) tačka funkcija , ako postoji takva okolina tačke da je za sve tačke iz ovog okruženja nejednakost ![]() , (
, (![]() ).
).
Minimalne i maksimalne tačke funkcije pozvao ekstremne tačke, a vrijednosti funkcije u tim tačkama su ekstremi funkcije(minimum i maksimum).
Imajte na umu da minimum i maksimum funkcije imaju lokalni karaktera, budući da se vrijednost funkcije u tački uspoređuje s njenim vrijednostima u tačkama koje su dovoljno blizu .
Teorema 1(neophodni ekstremni uslovi). Ako a je tačka ekstrema diferencijabilne funkcije, tada su njeni parcijalni derivati i u ovoj tački jednaki nuli: ![]()
![]() .
.
Pozivaju se tačke u kojima su parcijalni derivati prvog reda jednaki nuli kritičan ili stacionarno. U kritičnim tačkama, funkcija može ili ne mora imati ekstrem.
Teorema 2(dovoljan uslov ekstrema). Neka je funkcija : a) definirana u nekom susjedstvu kritične tačke, gdje je ![]() i
i ![]() ; b) ima kontinuirane parcijalne izvode drugog reda
; b) ima kontinuirane parcijalne izvode drugog reda ![]()
![]()
![]() . Onda ako
. Onda ako ![]() , tada funkcija u tački ima ekstrem: maksimum ako je A<0; минимум, если А>0; ako
, tada funkcija u tački ima ekstrem: maksimum ako je A<0; минимум, если А>0; ako ![]() , tada funkcija nema ekstrem u tački. Kada
, tada funkcija nema ekstrem u tački. Kada ![]() pitanje prisustva ekstremuma ostaje otvoreno.
pitanje prisustva ekstremuma ostaje otvoreno.
Prilikom proučavanja funkcije dvije varijable za ekstrem, preporučuje se korištenje sljedeće sheme:
1 Pronađite parcijalne izvode prvog reda: i .
2 Riješite sistem jednačina i pronađite kritične tačke funkcije.
3 Pronađite parcijalne izvode drugog reda: , , .
4 Izračunajte vrijednosti parcijalnih izvoda drugog reda u svakoj
kritičnu tačku i, koristeći dovoljne uslove, izvući zaključak o prisustvu ekstremuma.
5 Pronađite ekstreme funkcije.
Primjer 6 Pronađite ekstreme funkcije ![]() .
.
Odluka:
1 Pronalaženje parcijalnih izvoda i :
; ![]() .
.
2 Da bismo odredili kritične tačke, rešavamo sistem jednačina:
 ili
ili 
Iz prve jednadžbe sistema nalazimo: . Zamjena pronađene vrijednosti y u drugu jednačinu dobijamo:
, , ![]() ,
,
![]() .
.
Pronalaženje vrijednosti y, što odgovara vrijednostima ![]() . Zamjenjivanje vrijednosti
. Zamjenjivanje vrijednosti ![]() u jednadžbu , dobijamo: ; Tabela osnovnih neodređenih integrala ispunjava jednakost.
u jednadžbu , dobijamo: ; Tabela osnovnih neodređenih integrala ispunjava jednakost.
Odluka. Razlikujemo rezultat integracije:
 .
.
Dobili smo integrand, dakle, integracija je izvedena ispravno.
Definicija 25.7.
Funkcija se pozivakontinuirano u tački ako je definirana u nekom susjedstvu ove tačke (uključujući i samu tačku) i granica funkcije u ovoj tački postoji i jednaka je vrijednosti funkcije u ovoj tački, tj.
![]() ili
ili ![]() .
.
Primjer 25.3.
1) je kontinuiran u bilo kojoj tački.
2)

Ograničenje ne postoji za , tj. (0,0) – tačka prekida.
Osnovna svojstva kontinuiranih funkcija dviju varijabli
Definicija 25.8.
Skup tačaka u ravni se zovepovezan ako se bilo koje dvije tačke ovog skupa mogu povezati pravom.
Definicija 25.9.
Tačka se zoveinterni tačka skupa, ako postoji, koja se sastoji od tačaka datog skupa.
Definicija 25.10.
Povezani, otvoreni skup (koji se sastoji samo od unutrašnjih tačaka) se zoveotvoren područje ili samo područje
(na primjer, unutrašnjost kruga).
Definicija 25.11.
Tačka se zovegranica tačka regiona, ako u bilo kojoj postoje tačke, koje joj pripadaju i ne pripadaju. Skup svih graničnih tačaka ovog regiona se zovegranica oblasti. Oznaka: .

Definicija 25.12.
Skup tačaka formiranih od regije i njene granice se nazivazatvoreno području.
Definicija 25.13.
Skup se zoveograničeno ako postoji krug koji ga sadrži.
Napomena 4. Zatvoreno ograničeno područje u kojem je definirana funkcija dvije varijable je analog segmenta za funkciju jedne varijable.
1) Ako je funkcija kontinuirana u zatvorenom ograničenom domenu, onda ![]() .
.
2) Ako je funkcija kontinuirana u zatvorenom ograničenom području, tada ona dostiže svoje tačne strane u ovom području.
3) Funkcija kontinuirana u domeni preuzima sve svoje međuvrijednosti, tj. ako
Parcijalni derivati
Neka je funkcija definirana u susjedstvu tačke. Postavimo inkrement na varijablu u tački, ostavljajući ga nepromijenjenim, tj. pređimo na tačku koja pripada području (domen funkcije).
Definicija 26.1.
naziva se djelimično povećanje u odnosu na varijablu u tački
Definicija 26.2.
Ako postoji granica, onda se zoveparcijalni derivat funkcije u tački po varijabli.
Oznaka: ![]() .
.
Slično definisano
Ako uzmemo u obzir parcijalni izvod u odnosu na varijablu u bilo kojoj tački domene funkcije u domeni, onda se parcijalni izvod mogu smatrati novim funkcijama u domeni.
Dakle, parcijalni izvod funkcije dvije varijable u odnosu na varijablu je običan izvod jedne varijable po fiksnoj vrijednosti.
Primjer 26.1.
Naći parcijalne izvode funkcija: ,,.
 .
.
Koncept diferencijabilnosti funkcije dvije varijable
Definicija 26.3.
Neka je funkcija definirana, dakle
- puni inkrement funkcije.
Definicija 26.4.
Neka je funkcija definirana u susjedstvu tačke.
Funkcija se pozivadiferencibilan u tački ako se njegov ukupni prirast u ovoj tački može predstaviti kao:
gdje su konstante, su infinitezimalne funkcije za .
Teorema 26.1.
Ako je funkcija diferencibilna u nekoj tački, onda je kontinuirano na ovom mjestu.
Dokaz.
Očigledno iz (26.1): .
Teorema 26.2 (neophodan uslov za diferencijabilnost).
Ako je funkcija diferencijabilna u nekoj tački, tada ima parcijalne izvode u toj tački, i:
![]()
![]() .
(26.2)
.
(26.2)
Dokaz.
Neka vrijedi formula (26.1).
stavimo ,
gdje je at infinitezimalna funkcija.
Dijelimo sa , i prelazimo na granicu na, dobivamo:
odnosno, parcijalni izvod u odnosu na varijablu postoji i jednak je.
Slično se dokazuje i druga jednakost.
Napomena 1. Iz kontinuiteta ne radi to njegova diferencijabilnost!
Primjer 26.2.
je kontinuiran na (0,0), ali ![]() ne postoji.
ne postoji.
Slično, ne postoji parcijalni izvod u odnosu na . Dakle, funkcija nije diferencibilna.
Napomena 2. Iz postojanja parcijalnih derivata ne radi to diferencijabilnost funkcije.
Primjer 26.3.
Funkcija  ima parcijalne izvode u tački (0,0),
ima parcijalne izvode u tački (0,0),
ali nije kontinuirano u ovom trenutku, stoga -
nije diferenciran.
Teorema 26.3 (dovoljan uslov za diferencijabilnost).
Ako funkcija ima parcijalne izvode u nekoj okolini tačke, a ovi izvodi su neprekidni u samoj tački, tada je funkcija diferencijabilna u toj tački.
Posljedica.
Ako su parcijalne derivacije kontinuirane, onda je funkcija kontinuirana.
Definicija 26.5.
Ako je funkcija diferencijabilna u nekoj tački, onda se poziva diferencijallinearno s obzirom na prirast, dio ukupnog prirasta ove funkcije u tački, tj.
, ili
Diferencijali nezavisnih varijabli su njihovi priraštaji
Derivat složene funkcije dvije varijable
Neka je funkcija dvije varijable, a svaka od njih je funkcija varijable:.
Tada je kompleksna funkcija varijable.
Teorema 26.4.
Ako su funkcije diferencibilne u nekoj tački,
je diferencibilna u točki , onda je kompleksna funkcija također diferencibilna u točki. pri čemu:
![]() (26.4)
(26.4)
Primjer 26.4.
2)
![]()
 .
.
Napomena 3.
Ako i tada ![]() .
.
Gradijent(od lat. gradijenti, rod. slučaj gradientis- hodanje, rast) - vektor, čiji smjer pokazuje smjer najbržeg povećanja određene veličine, čija se vrijednost mijenja od jedne tačke u prostoru do druge (skalarno polje), a po veličini (modulu) jednaka je stopa rasta ove količine u ovom pravcu.
Na primjer, ako uzmemo za visinu Zemljine površine iznad nivoa mora, tada će njen gradijent u svakoj tački površine pokazati "smjer najstrmijeg uspona" i karakterizirati strminu padine svojom veličinom.
Za slučaj trodimenzionalnog prostora, gradijent skalara funkcije
![]() koordinate, naziva se vektorska funkcija sa komponentama
koordinate, naziva se vektorska funkcija sa komponentama
Ili, koristeći za jedinične vektore duž osi pravokutnih kartezijanskih koordinata:
Ako je funkcija varijabli, tada je njen gradijent -dimenzionalni vektor

čije su komponente jednake privatni derivat za sve njene argumente.
Značenje gradijenta bilo koje skalarne funkcije je da njen skalarni proizvod sa beskonačno malim vektorom pomaka daje totalni diferencijal ove funkcije sa odgovarajućom promjenom koordinata u prostoru na kojem je definiran, odnosno linearni (u slučaju generalnog položaja to je i glavni) dio promjene kada se pomakne na. Koristeći isto slovo za označavanje funkcije vektora i odgovarajuće funkcije njegovih koordinata, može se napisati:
Ovdje je vrijedno napomenuti da budući da formula za ukupni diferencijal ne ovisi o vrsti koordinata, odnosno o prirodi parametara x općenito, onda je rezultirajući diferencijal invarijanta, odnosno skalar, za bilo koje transformacije koordinata, a budući da je to vektor, ispada gradijent izračunat na uobičajeni način kovarijantni vektor, odnosno vektor predstavljen u dualnoj bazi, koji samo skalar može dati jednostavnim zbrajanjem proizvoda koordinata uobičajenog ( kontravarijantno), odnosno vektor napisan u uobičajenoj osnovi. Dakle, izraz (općenito govoreći, za proizvoljne krivolinijske koordinate) može se sasvim ispravno i nepromjenjivo napisati kao:
![]()
ili, izostavljajući znak zbira prema Einsteinovom pravilu,
![]()
(u ortonormalnoj osnovi, možemo pisati sve indekse kao indekse, kao što smo uradili gore). Međutim, ispada da je gradijent pravi kovarijantni vektor u svim krivolinijskim koordinatama.
linija nivoa funkcije je skup tačaka iz svoje domene definicije u kojima funkcija uzima istu fiksnu vrijednost. Gradijent funkcije f(x) zove vektor

Δ f(x) =df ,…, df
dx 1 dx n
koji ukazuje na smjer najbržeg porasta funkcije, te stoga orijentiran okomito na linije nivoa.
Za linearnu funkciju dvije varijable, linija nivoa je prava linija okomita na vektor sa, koji služi kao gradijent ove funkcije. Dakle, ako je linija nivoa data jednadžbom f(x)=c 1 x 1 +c 2 x 2 =konst, tada ovaj vektor ima oblik
i ukazuje na smjer rastuće funkcije.
Dakle, sa geometrijske tačke gledišta, problem maksimizacije se svodi na određivanje takve tačke domene D, kroz koji prolazi linija nivoa, što odgovara najvećoj mogućoj vrijednosti. Potonje znači da da bismo pronašli tačku ekstrema u problemu linearnog programiranja, prvo moramo konstruirati liniju nivoa za neku proizvoljnu vrijednost ciljne funkcije. Zatim je potrebno izvršiti njegovo paralelno kretanje (tako da ostane okomito na vektor sa) dok ne dođemo do takve tačke u domenu prihvatljivih planova D, od kojeg je pomak u smjeru vektora sa bilo bi nemoguće. Ova metoda rješenja se zove grafički. Napominjemo da se rješavanje problema pronalaženja minimuma linearne funkcije izvodi na sličan način, s jedinom razlikom što kretanje duž linija nivoa treba vršiti u smjeru suprotnom od gradijenta ciljne funkcije, tj. duž vektora (-sa).
Na pirinač. 1.1 prikazan je neki poseban slučaj za koji se rješenje LLP-a postiže u kutnoj tački X*= (0, 6) oblasti D. Nije teško zamisliti da su moguće i druge opcije. Oni su prikazani na pirinač. 1.2.
Slika ( a) ilustruje situaciju neograničenosti ciljne funkcije f(x)=cx na setu D, tj. bez obzira koliko se krećemo duž linija nivoa u pravcu vektora sa, njegova vrijednost će se povećati.
U slučaju prikazanom na slici ( b), linija nivoa koja odgovara maksimalnoj vrijednosti f(x), dodiruje ivicu seta D, i, shodno tome, sve tačke koje leže na ovom licu su optimalni planovi.
U svim razmatranim ilustracijama, dozvoljeni planovi LLP-a su predstavljeni kao neki poliedarski konveksni skup na ravni. Ovaj prikaz u literaturi se zove prva geometrijska interpretacija problema linearnog programiranja.
Definicija 1. Broj ALI naziva se granica funkcije u točki (ili u i ) ako za bilo koji proizvoljno mali pozitivan broj postoji pozitivan broj takav da za sve točke udaljene od točke na udaljenosti manjoj od , nejednakost
Ograničenje je naznačeno.
Definicija 2. Funkcija
se kaže da je kontinuirana u nekoj tački ako granica funkcije postoji u toj tački i ![]() .
.
Tačke u kojima funkcija nema svojstvo kontinuiteta nazivaju se tačke diskontinuiteta.
Sva svojstva i metode teorije granica funkcije jedne varijable prenose se na funkcije više varijabli.
2) Slučajna varijabla je jedan od osnovnih koncepata teorije vjerovatnoće. Slučajna varijabla je mjerljiva funkcija data na nekom prostoru vjerovatnoće
Diskretna je slučajna varijabla koja tokom testiranja može poprimiti jednu od izolovanih vrijednosti čiji je broj konačan. To uključuje vrijednosti iz prve grupe.
Kontinuirana varijabla je slučajna varijabla koja, unutar granica svoje promjene, može poprimiti bilo koju vrijednost koja može biti konačna ili beskonačna. To uključuje količine iz druge grupe.
Ulaznica broj 6
1) Eksponencijacija- binarna operacija, izvorno izvedena iz višestrukog množenja prirodnog broja sam po sebi. Oznaka: zv stepen sa osnovu i indikator .
Formula De Moivre za kompleksne brojeve kaže da
za bilo koga
Formula je dobila ime po matematičaru I. Moivreu, koji ju je uspostavio 1707. godine, prijatelju velikog I. Newtona; L. Euler je formuli dao moderan izgled.
Dokaz [uredi]
De Moivreova formula odmah slijedi iz Eulerove formule i identiteta za eksponent , gdje b je cijeli broj.
Aplikacija [uredi]
Slična formula je također primjenjiva pri izračunavanju korijena n stepen iz kompleksnog broja različitog od nule:
gdje k = 0, 1, …, n-1.
Vjerovatnoća hipoteza
Vjerovatnoća hipoteza.
Neka se događaj A može desiti pod uslovom da se pojavi jedan od nekompatibilnih događaja B1, B2,?Bn, koji formira kompletnu grupu. Budući da se unaprijed ne zna koji će se od ovih događaja dogoditi, oni se nazivaju hipotezama. Vjerovatnoća pojave događaja A određena je formulom ukupne vjerovatnoće:
R(A) = R(V1)?RV1(A) + R(V2) ?RV2(A)+ ? +R(Vn) ?RVn(A)
Bayesova formula:
![]() ,
,
Prethodna vjerovatnoća hipoteze A(vidi dolje za značenje takve terminologije);
Vjerojatnost hipoteze A kada se dogodi neki događaj B(posteriorna vjerovatnoća);
Vjerovatnoća događaja B ako je hipoteza tačna A;
Ukupna vjerovatnoća da će se događaj dogoditi B.
primjer:
Primjer izračuna
Neka je vjerovatnoća braka za prvog radnika , za drugog radnika - , a za trećeg - . Prvi je napravio dijelove, drugi je napravio dijelove, a treći je napravio dijelove. Predradnik uzima nasumce i ispostavi se da je neispravan. Postavlja se pitanje kolika je vjerovatnoća da je ovaj dio napravio treći radnik?
Događaj - dio braka, događaj - dio je proizveo radnik. Onda ![]() , gdje , i
, gdje , i ![]() . Prema formuli ukupne vjerovatnoće
. Prema formuli ukupne vjerovatnoće

Prema Bayesovoj formuli dobijamo:
Ulaznica broj 12
1. Trigonometrijski Fourierov niz- predstavljanje proizvoljne funkcije sa periodom kao niz
kvote ao,an i bn nazivaju se Fourierovi koeficijenti, a ako se mogu naći, onda se niz (1) naziva Fourierov red koji odgovara funkciji f(x). Za niz (1), pojam (a1cosx+b1sinx) se naziva prvi ili osnovni harmonik,
Fourierovi nizovi periodičnih funkcija s periodom 2π.
Fourierova serija
Standardna (=uobičajena) notacija kroz zbir sinx i cosx
f(x)=ao+ a1cosx+a2cos2x+a3cos3x+...+b1sinx+b2sin2x+b3sin3x+...,
gdje su ao, a1,a2,...,b1,b2,.. realne konstante, tj.

2.suprotnih događaja.
Nasuprot navedite dva jedinstveno moguća događaja koji čine kompletnu grupu. Ako je jedan od dva suprotna događaja označen sa A, tada je uobičajeno da se označi drugi
Teorema. Zbir vjerovatnoća suprotnih događaja jednak je jedan:
![]()
Primjer 1 Pogađanje i promašaj prilikom gađanja mete su suprotni događaji. Ako je A pogodak, onda je suprotan događaj promašaj.
Primjer 2 Jedan dio je nasumično uzet iz kutije. Događaji “pojavio se standardni dio” i “pojavio se nestandardni dio” su suprotni
, očigledno je jednako 10/21, što je gore navedeno. [ 1 ]
Izračunaj verovatnoća suprotnog događaja O. Događaj je da odabrani broj ne sadrži nijednu od tri date cifre. [ 2 ]
Suma vjerovatnoće suprotnih događaja je jednako jedan. [ 3 ]
Gde verovatnoća suprotnog događaja A će biti veće od 1-a, odnosno biće onoliko blizu jedan koliko je vjerovatnoća događaja A blizu nuli
Ulaznica broj 9
1. Frekvencijski poligon se naziva polilinija čiji segmenti spajaju tačke ( x 1 ; n 1 ), (x2 ; n 2 ), ..., (x k ; nk ). Za izgradnju poligona frekvencija na osi apscise, opcije su ostavljene po strani x i , a na y-osi - odgovarajuće frekvencije n i . Poeni ( x i ; n i ) su povezani segmentima pravih linija i dobijaju poligon frekvencija
histogram frekvencije naziva se stepenasta figura koja se sastoji od pravougaonika čije su osnove parcijalni intervali dužine h , a visine su jednake omjeru n i / h (gustina frekvencije).
2. Događaji ALI i AT nazivaju se nezavisnim ako P(AB) = P(A) P(B). Više događaja ALI, AT, With,... nazivaju se nezavisnim ako je vjerovatnoća njihove zajedničke implementacije jednaka umnošku vjerovatnoća svakog od njih posebno: R(ABC…) = R(ALI)R(AT)R(With)…
Ponekad omjer R(AB) = R(ALI) R(AT|A) = P(B)P(A|B), važi za P(A)P(B) > 0, također se naziva teorema množenja vjerovatnoće
Ulaznica broj 11
1) Slučajna varijabla X naziva se kontinuirana (kontinuirano raspoređena) varijabla ako postoji takva nenegativna funkcija p(t) definirana na cijeloj realnoj osi da je za sve x funkcija distribucije slučajne varijable F(x) jednak:
. ![]()
U ovom slučaju, funkcija p(t) se naziva gustinom raspodjele vjerovatnoće kontinuirane slučajne varijable.
Ako takva funkcija p(t) ne postoji, tada X nije kontinuirano distribuirana slučajna varijabla.
Dakle, znajući gustinu distribucije, po formuli (6.7) se lako može naći funkcija raspodjele F(x). I obrnuto, iz poznate funkcije distribucije, može se vratiti gustina distribucije:
Svojstva gustoće vjerovatnoće
kontinuirana slučajna varijabla:
1. Gustoća distribucije je nenegativna funkcija:
Geometrijski, to znači da se dijagram gustine raspodjele nalazi ili iznad ose Ox, ili na ovoj osi.
Uzimajući u obzir da je F(+¥)=1, dobijamo: =1. One. površina između dijagrama gustine vjerovatnoće i x-ose je jednaka jedan.
Ova dva svojstva su karakteristična za gustinu raspodjele vjerovatnoće. Dokazana je i suprotna tvrdnja:
Zbir događaja A i B je treći događaj A + B, koji se događa ako i samo ako se dogodi barem jedan od događaja: A ili B.
Proizvod događaja A i B je treći događaj AB, koji se dešava ako i samo ako oba događaja: A i B.
Koncepti zbira i proizvoda dvaju događaja očito se prenose na slučaj bilo kojeg skupa događaja.
Događaj suprotan događaju A je događaj koji se događa ako i samo ako se događaj A ne dogodi.