Linearna aproksimacija po komadima. Aproksimacija funkcije pomoću linije trenda Aproksimacija linearne funkcije
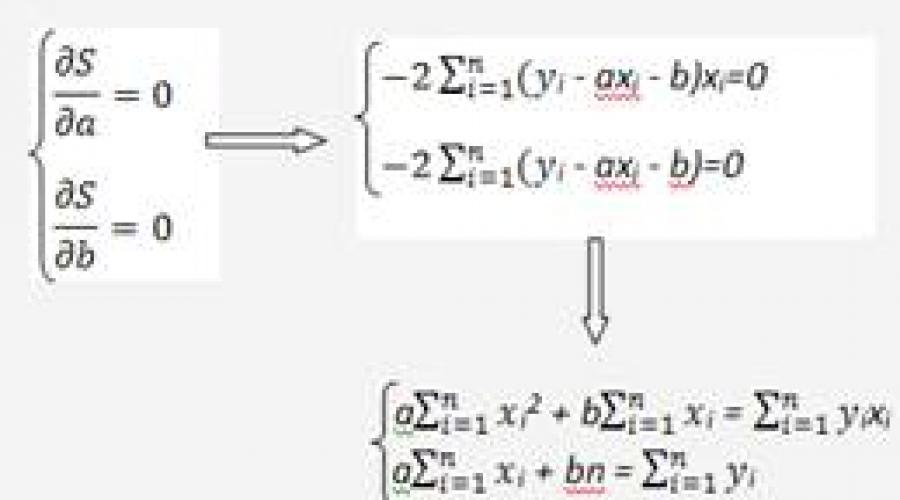
Pročitajte također
Linearna aproksimacija- (Linearna aproksimacija) – vidi Aproksimacija, Linearnost u ekonomiji...
linearna aproksimacija- linearna aproksimacija Aproksimacija je približan izraz bilo koje veličine ili objekta u terminima drugih jednostavnijih veličina ili objekata. U slučaju linearne aproksimacije, aproksimacija se gradi korištenjem linearnih funkcija. ] Teme informaciona sigurnost EN linearna aproksimacija blok šifri… Priručnik tehničkog prevodioca
komadno linearna aproksimacija funkcije- - [L.G. Sumenko. Engleski ruski rječnik informacionih tehnologija. M.: GP TsNIIS, 2003.] Teme informatičke tehnologije općenito EN komadno linearna aproksimacija ... Priručnik tehničkog prevodioca
Aproksimacija- "zamjena nekih matematičkih objekata drugim, u ovom ili onom smislu bliskim izvornim"; posebno, aproksimativni izraz složene funkcije koristeći jednostavnije. Na primjer, s komadno linearnim A., kontinuiranim ... ... Ekonomsko-matematički rječnik
aproksimacija- "Zamjena nekih matematičkih objekata drugim, u ovom ili onom smislu bliskim originalu" . Konkretno, približan izraz složene funkcije uz pomoć jednostavnijih. Na primjer, s komadno linearnim A., kontinuiranim ... ... Priručnik tehničkog prevodioca
Grupa linearnih transformacija vektorskog prostora V konačne dimenzije n nad nekim tijelom K. Izborom baze u prostoru V ostvaruje se L. r. Mathematical Encyclopedia
Numeričke metode rješavanja metoda koje omogućavaju dobivanje rješenja od L. do. z. u obliku tablice njegovih približnih vrijednosti u tačkama mreže, bez korištenja preliminarnih informacija o očekivanom obliku rješenja. Za teoriju ovih metoda tipična je pretpostavka da ... Mathematical Encyclopedia
Metoda za rješavanje klase zadataka statistike. evaluacija, u kojoj je nova vrijednost procjene prilagođavanje već postojeće procjene, na osnovu novog zapažanja. Prvi postupak S. i. predložili su 1951. X. Robbins (N. Robbins) i S. Monroe ... ... Mathematical Encyclopedia
linearna algebarska numerička metoda
Često, kada se analiziraju eksperimentalni podaci, postaje potrebno pronaći funkcionalni odnos između vrijednosti x i y, koje se dobiju kao rezultat mjerenja. Analitička studija odnosa između dvije vrijednosti x i y proizvodi tablicu vrijednosti, koja se može prikazati i grafički.
Ako je, međutim, poznat oblik aproksimirajuće funkcije, onda se problem aproksimacije svodi samo na pronalaženje koeficijenata (a, b, c,...) uključenih u funkciju. Za pronalaženje ovih koeficijenata koristi se metoda najmanjih kvadrata koja se sastoji u tome da se zbroj kvadrata vertikalnih udaljenosti od tačaka do grafa funkcije y=f(x, a, b, c,.. .) je najmanji: S = i 2 = min, gdje je S i = y i - f(x i , a, b, c,...). Da bismo to učinili, koristimo neophodan uslov za ekstremum funkcije nekoliko varijabli i - f(x i , a, b, c,...)) 2: jednakost nuli parcijalnih izvoda. Rezultat je sistem. Dakle, pronalaženje koeficijenata se svodi samo na rješavanje sistema:
Linearna regresija
Linearna funkcija ima oblik y = ax + b, stoga je potrebno pronaći dva parametra: a i b, uz uslov da su date koordinate n tačaka pronađenih eksperimentalno sa slučajnim greškama („šum“). Da bismo to učinili, sastavljamo funkciju i - (ax i + b)) 2 , otvaramo zagrade i - ax i - b) 2 i sastavljamo sistem:
Neka A = i, B = i, C = i x i, D = i 2, tada će sistem poprimiti oblik:

Ovaj sistem linearnih algebarskih jednadžbi rješavamo Cramer metodom i na taj način pronalazimo željene vrijednosti parametara a i b:

Table. Postoje tačke:
Koristeći metodu izračunavanja parametara linearne funkcije, dobijamo:
a = 0,1215455 , b = - 0,2140002
Primjer.
Eksperimentalni podaci o vrijednostima varijabli X i at date su u tabeli. 
Kao rezultat njihovog usklađivanja, funkcija ![]()
Koristeći metoda najmanjeg kvadrata, aproksimira ove podatke linearnom zavisnošću y=ax+b(pronađi opcije a i b). Saznajte koja od dvije linije je bolja (u smislu metode najmanjih kvadrata) poravnava eksperimentalne podatke. Napravite crtež.
Suština metode najmanjih kvadrata (LSM).
Problem je pronaći koeficijente linearne zavisnosti za koje je funkcija dvije varijable a i b ![]() uzima najmanju vrijednost. Odnosno, s obzirom na podatke a i b zbir kvadrata odstupanja eksperimentalnih podataka od pronađene prave će biti najmanji. Ovo je cijela poenta metode najmanjih kvadrata.
uzima najmanju vrijednost. Odnosno, s obzirom na podatke a i b zbir kvadrata odstupanja eksperimentalnih podataka od pronađene prave će biti najmanji. Ovo je cijela poenta metode najmanjih kvadrata.
Dakle, rješenje primjera se svodi na pronalaženje ekstrema funkcije dvije varijable.
Izvođenje formula za pronalaženje koeficijenata.
Sastavlja se i rješava sistem dvije jednačine sa dvije nepoznate. Pronalaženje parcijalnih izvoda funkcije u odnosu na varijable a i b, izjednačavamo ove izvode sa nulom. 
Rezultirajući sistem jednačina rješavamo bilo kojom metodom (npr metoda zamjene ili ) i dobiju formule za pronalaženje koeficijenata koristeći metodu najmanjih kvadrata (LSM). 
Sa podacima a i b funkcija ![]() uzima najmanju vrijednost. Dokaz ove činjenice je dat.
uzima najmanju vrijednost. Dokaz ove činjenice je dat.
To je cijela metoda najmanjih kvadrata. Formula za pronalaženje parametra a sadrži sume , , , i parametar n- količina eksperimentalnih podataka. Vrijednosti ovih suma se preporučuje da se izračunaju zasebno. Koeficijent b pronađeno nakon proračuna a.
Vrijeme je da se prisjetimo originalnog primjera.
Odluka.
U našem primjeru n=5. Popunjavamo tabelu radi praktičnosti izračunavanja iznosa koji su uključeni u formule potrebnih koeficijenata. 
Vrijednosti u četvrtom redu tabele dobijaju se množenjem vrijednosti 2. retka sa vrijednostima 3. reda za svaki broj i.
Vrijednosti u petom redu tabele dobijaju se kvadriranjem vrijednosti 2. reda za svaki broj i.
Vrijednosti posljednje kolone tabele su zbroji vrijednosti u redovima.
Za pronalaženje koeficijenata koristimo formule metode najmanjih kvadrata a i b. U njih zamjenjujemo odgovarajuće vrijednosti iz posljednje kolone tabele: 
dakle, y=0,165x+2,184 je željena aproksimirajuća ravna linija.
Ostaje da saznamo koja od linija y=0,165x+2,184 ili ![]() bolje aproksimira originalne podatke, tj. da procjenu metodom najmanjih kvadrata.
bolje aproksimira originalne podatke, tj. da procjenu metodom najmanjih kvadrata.
Procjena greške metode najmanjih kvadrata.
Da biste to učinili, morate izračunati sume kvadrata odstupanja izvornih podataka od ovih linija ![]() i
i ![]() , manja vrijednost odgovara liniji koja bolje aproksimira originalne podatke u smislu metode najmanjih kvadrata.
, manja vrijednost odgovara liniji koja bolje aproksimira originalne podatke u smislu metode najmanjih kvadrata. 
Od , onda linija y=0,165x+2,184 bolje aproksimira originalne podatke.
Grafička ilustracija metode najmanjih kvadrata (LSM).
Na listama sve izgleda odlično. Crvena linija je pronađena linija y=0,165x+2,184, plava linija je ![]() , ružičaste tačke su originalni podaci.
, ružičaste tačke su originalni podaci.

Čemu služi, čemu sve ove aproksimacije?
Ja lično koristim za rješavanje problema izglađivanja podataka, problema interpolacije i ekstrapolacije (u originalnom primjeru od vas bi se moglo tražiti da pronađete vrijednost uočene vrijednosti y at x=3 ili kada x=6 prema MNC metodi). Ali o tome ćemo više govoriti kasnije u drugom dijelu stranice.
Dokaz.
Tako da kada se nađe a i b funkcija uzima najmanju vrijednost, potrebno je da u ovom trenutku matrica kvadratnog oblika diferencijala drugog reda za funkciju ![]() bilo pozitivno određeno. Hajde da to pokažemo.
bilo pozitivno određeno. Hajde da to pokažemo.
Odjeljenje: ________ Informatika i računarska tehnologija _______________
NASTAVNI RAD
po disciplini _______________ INFORMATIKA __________________________
(naziv nastavne discipline prema nastavnom planu i programu)
VJEŽBA
student IHL-12 grupe Rumjancev N.A.
(šifra grupe) (puno ime)
1. Predmet rada: _ Implementacija numeričke metode korišćenjem Microsoft Excel-a i korišćenjem alata MathCAD paketa
2. Početni podaci za rad: _Opcija br. 17_______________________________________
4. Spisak grafičkog materijala: _ Prezentacija rezultata u obliku ekranskih formulara________________________________ ____________________________________
5. Rok za izvršenje radova: ___ 05.01.2013 ____________________________
Rukovodilac rada: ________ ______________ /_________/
(pozicija) (potpis) (puno ime)
Datum izdavanja zadatka: __ 15. februara 2013 ______________
anotacija
Obrazloženje je izvještaj o realizaciji nastavnog rada. Razmatra se pitanja pronalaženja empirijskih formula metodom najmanjih kvadrata (LSM) uz korištenje mogućnosti Microsoft Excel paketa, a razmatra se i rješenje ovog problema u MathCAD paketu. U radu su dobijene jednačine različitih tipova aproksimacijom linearnih, kvadratnih i eksponencijalnih zavisnosti. Na kraju rada zaključeno je koja metoda je najbolje riješila problem.
Strane 24, tabele 3, slike 14, aplikacije 0.
Sažetak
Obrazloženje predstavlja izvještaj o uspješnosti seminarskog rada. U njemu se razmatraju pitanja o pronalaženju empirijskih formula metodom najmanjih kvadrata (OLS) uz pomoć mogućnosti paketa Microsoft Excel, a razmatra se i rješavanje datog problema u Turbo Pascalu 7.0. U radu su dobijene jednačine različitih vrsta pomoću aproksimacijskih linearnih, kvadratno-zakonskih i eksponencijalnih ovisnosti. Po završetku rada donosi se zaključak, rješava se problem koji je metod bolji.
Strane 24, tabele 3, slike 14, dodaci 0.
Anotacija. 2
Uvod. 4
Formulacija problema. 5
Opće informacije. 6
Linearna zavisnost. 7
Nelinearna zavisnost. 7
Početni podaci. deset
Izračunavanje aproksimacija u Excel 11 proračunskoj tabeli
Konstrukcija grafova. 17
LINEST funkcija 18
Aproksimacija u MathCAD-u.. 19
Uvod. devetnaest
Linearna aproksimacija u MathCAD-u.. 21
Eksponencijalna aproksimacija u MathCAD-u.. 22
Polinom (kvadratna aproksimacija u MathCAD-u.. 23
Reference.. 24
Uvod
Aproksimacija (od latinskog "approximare" - "pristup") je naučna metoda čija je suština zamjena nekih poznatih vrijednosti drugim, približnim i jednostavnijim. Ove jednostavne vrijednosti moraju zadovoljiti neku ovisnost, čije je pronalaženje, općenito, krajnji cilj ove metode.
Poznato je da funkcionalna zavisnost između veličina može biti ili egzaktna (ovaj slučaj je tipičan za teorijske pronalaske) ili približna (što je tipičnije za eksperimentalno dobijene podatke). Ova nepreciznost, odstupanje dobijene vrednosti od željene zavisnosti, koja se na grafu iskazuje kao raspršivanje tačaka na određenoj udaljenosti od krive (ovde malo preterujem) može imati nekoliko razloga:
1. Greške u direktnim mjerenjima (instrumentalne), ljudske greške (ovdje, naravno, ne govorim o grubim greškama koje daju značajna odstupanja).
2. Nesavršenstvo ljudskog znanja o prirodi - nikako nam ne dozvoljavaju svi moderni naučni koncepti da precizno izračunamo bilo koje vrijednosti za stvarne slučajeve - mnogi od njih su usmjereni na idealne slučajeve.
3. Složenost i varijabilnost same prirode (posebno žive). Na primjer, u slučaju socioloških istraživanja, tačna podudarnost između eksperimentalnih i teorijskih podataka uopće nije potrebna - čak i mala korelacija eksperimentalnih rezultata s očekivanim obrascima već može mnogo reći stručnjacima.
Prilikom odabira aproksimacije treba polaziti od specifičnog zadatka studije. Obično, što je jednačina koja se koristi za aproksimaciju jednostavnija, to je dobijeni opis zavisnosti približniji. Stoga je važno pročitati koliko su značajna i što je uzrokovalo odstupanja konkretnih vrijednosti od rezultirajućeg trenda. Kada se opisuje zavisnost empirijski utvrđenih vrednosti, mnogo veća tačnost se može postići upotrebom neke složenije, višeparametarske jednačine. Međutim, nema smisla pokušavati prenijeti nasumična odstupanja vrijednosti u određenim serijama empirijskih podataka s maksimalnom preciznošću. Mnogo je važnije uhvatiti opštu pravilnost, koja je u ovom slučaju najlogičnije i sa prihvatljivom tačnošću izražena upravo dvoparametarskom jednačinom funkcije stepena. Stoga, prilikom odabira metode aproksimacije, istraživač uvijek pravi kompromis: odlučuje u kojoj mjeri je u ovom slučaju svrsishodno i prikladno „žrtvovati“ detalje i, shodno tome, koliko generalizirano treba izraziti ovisnost upoređenih varijabli. Uz identifikaciju obrazaca maskiranih slučajnim odstupanjima empirijskih podataka od opšteg obrasca, aproksimacija omogućava i rješavanje mnogih drugih važnih problema: formalizirati pronađenu ovisnost; pronađite nepoznate vrijednosti zavisne varijable interpolacijom ili, ako je primjenjivo, ekstrapolacijom.
Formulacija problema
1. Koristeći metodu najmanjih kvadrata, aproksimiramo funkciju datu u tabeli
a) polinom prvog stepena ![]() ;
;
b) polinom drugog stepena;
c) eksponencijalna zavisnost.
2. Izračunajte koeficijent determinizma za svaku zavisnost.
3. Izračunajte koeficijent korelacije (samo u slučaju a).
4. Za svaku zavisnost napravite liniju trenda.
5. Pomoću funkcije LINEST izračunajte numeričke karakteristike zavisnosti y od x.
6. Uporedite svoje proračune s rezultatima dobivenim korištenjem funkcije LINEST.
7. Zaključiti koja od dobijenih formula najbolje aproksimira funkciju .
8. Obraditi date eksperimentalne podatke pomoću ugrađenih funkcija interpolacije (aproksimacije) i regresije MathCAD paketa i uporediti rezultate sa rezultatima dobijenim u programu Microsoft Excel.
Opće informacije
U eksperimentalnom istraživanju funkcionalne zavisnosti y = f(x), vrijednost y mjeri se na različitim vrijednostima vrijednosti x. Rezultati su prikazani u obliku tabele 1 ili grafički.
| X | x 1 | x2 | ××× | x n |
| Y | x 1 | Y2 | ××× | y n |
Tabela 1
Zadatak je analitički prikazati željenu funkcionalnu zavisnost, tj. u odabiru formule koja opisuje rezultate eksperimenta. Empirijska formula se obično bira iz prilično uske klase funkcija, uzimajući u obzir, na primjer, skup linearnih, potencijskih, eksponencijalnih itd. funkcija. Istovremeno se rukovode nekim teorijskim razmatranjima ili razmatranjima jednostavnosti u predstavljanju empirijskog materijala. Pronađena empirijska formula treba biti takva da se vrijednosti funkcija izračunate iz nje pri X=x i mogu malo razlikovati od eksperimentalnih podataka y i (i = 1, 2, …, n).
Označiti izabranu funkcionalnu zavisnost
će biti minimalan. Dakle, parametri a 1 , a 2 , …, i m se određuju iz uslova da je zbir kvadrata odstupanja izmjerenih vrijednosti y i od ![]() uzeo najmanju vrijednost.
uzeo najmanju vrijednost.
Koristeći neophodne uslove za ekstremum funkcije nekoliko varijabli, dobijamo normalan sistem za određivanje koeficijenata a 1 , a 2 , ... i m
gdje su a1, a2 nepoznati parametri, a sistem (1.3) ima oblik
gdje su a, b konstante i x > 0 i y > 0.
Uzimajući logaritam jednakosti (1.2.1), dobijamo
i primjenom formula (1.1.2) nalazimo vrijednosti parametara b i u, a zatim vrijednost parametra a.
eksponencijalna zavisnost
Uz pretpostavku v = lny, c = lna, Y = x, dobijamo linearnu zavisnost
Tabela br. 3.6
Što je manja vrijednost Q, to bolje empirijska formula odgovara eksperimentalnim podacima.
U svakom zadatku, metodom najmanjih kvadrata potrebno je pronaći teorijsku funkcionalnu ovisnost za funkciju specificiranu u tablici. Kao teorijsku funkcionalnu zavisnost koristite:
– Polinom prvog stepena ![]() ,
,
– eksponencijalna funkcija,
– funkcija napajanja,
- Polinom drugog stepena.
Za svaku zavisnost pronađite teorijsku vrijednost funkcije, zbroj kvadrata odstupanja empirijskih vrijednosti funkcije od teoretskih vrijednosti, naznačite najmanju vrijednost ove vrijednosti i aproksimirajuću funkciju kojoj ona odgovara. Napravite liniju trenda za svaku zavisnost i prikažite jednadžbu ove linije na dijagramu. Pokažite na dijagramu vrijednost koeficijenta determinizma R 2 . Ovaj koeficijent se izračunava po formuli
 , ,
| (2.1) |
gdje su date vrijednosti funkcije,
Teorijske vrijednosti funkcije,
Aritmetička sredina, i = 1, 2, …, n.
Ako je koeficijent determinizma jednak 1, tada se teorijske i empirijske vrijednosti funkcije potpuno poklapaju. Ako je koeficijent
determinizma je 0, tada je teorijska zavisnost odabrana neuspješno.
Početni podaci
Neki eksperiment je napravljen. Njegovi rezultati se bilježe u obliku tabele, gdje je x i vrijednost koju je odredio istraživač (na primjer, koncentracija reagensa u hemijskom rastvoru), y i je izmjerena vrijednost (u našem primjeru, to može biti brzina reakcije ).
| x i | y i | x i | y i | x i | y i | x i | y i | x i | y i |
| 0.21 | 1.62 | 4.98 | 40.09 | 7.96 | 63.31 | 12.33 | 97.77 | 17.32 | 126.45 |
| 1.19 | 8.65 | 5.49 | 43.56 | 8.32 | 67.45 | 13.21 | 105.34 | 18.43 | 144.34 |
| 2.43 | 16.76 | 6.07 | 48.45 | 9.43 | 72.87 | 14.72 | 112.56 | 19.38 | 160.45 |
| 3.12 | 24.45 | 6.81 | 52.21 | 10.21 | 81.34 | 15.53 | 121.89 | 20.45 | 161.34 |
| 4.54 | 32.87 | 7.21 | 57.34 | 11.54 | 89.45 | 16.23 | 108.54 | 21.22 | 170.59 |
tabela 2
Izračunavanje aproksimacija u Excel tabeli
transkript
1 APROKSIMANJE FUNKCIJA. OSNOVNI POJMOVI I DEFINICIJE Izjava o problemu. Osnovu matematičkih modela mnogih procesa i pojava u fizici, hemiji, biologiji, ekonomiji i drugim oblastima čine jednačine različitih tipova: nelinearne jednačine, obične diferencijalne jednačine, parcijalne diferencijalne jednačine itd. Za rješavanje takvih jednadžbi potrebno je biti u stanju izračunati vrijednosti funkcija uključenih u opis matematičkog modela procesa ili pojave koja se razmatra, za proizvoljnu vrijednost argumenta. Za složene modele, takvi proračuni mogu biti dugotrajni čak i kada se koristi računar. Funkcije koje se koriste u matematičkim modelima mogu se specificirati i analitički (u obliku formule) i tabelarno, u kojima je funkcija poznata samo za određene diskretne vrijednosti argumenta. Konkretno, ako se funkcionalna ovisnost dobije kao rezultat proračuna izvedenih na računalu, ili u procesu mjerenja provedenih u okviru eksperimenta, onda se ispostavlja da je točno specificirana na tabelarni način. U praksi će nam možda trebati vrijednosti funkcije u drugim točkama od onih navedenih u tabeli. Međutim, ove vrijednosti se mogu dobiti samo složenim proračunima ili skupim eksperimentima. Dakle, sa stanovišta uštede vremena i novca, dolazimo do problema izračunavanja približnih vrijednosti funkcije za bilo koju vrijednost argumenta na osnovu dostupnih tabelarnih podataka. Ovaj problem se rješava aproksimativnom zamjenom funkcije jednostavnijom funkcijom, koju je lako izračunati za bilo koju vrijednost argumenta x u datom intervalu njegove promjene. Uvedena funkcija se može koristiti ne samo za približno određivanje numeričkih vrijednosti, već i za analitičke proračune u teorijskom proučavanju modela. Aproksimacija funkcije jednostavnijom funkcijom naziva se aproksimacija (od latinskog approximo pristupa). Aproksimirajuća funkcija je izgrađena na način da su odstupanja (u određenom smislu) od u datoj oblasti najmanja. Koncept malog odstupanja ovisi o tome kako se procjenjuje blizina dviju funkcija, pa će kasnije biti preciziran kada se razmatraju specifične metode aproksimacije. Kontinuirana aproksimacija. Ako je izvorna funkcija data analitičkim izrazom, tada je prilikom konstruiranja aproksimirajuće funkcije moguće zahtijevati minimalno odstupanje jedne funkcije od druge na nekom kontinuiranom skupu tačaka, na primjer, na segmentu. Ova vrsta aproksimacije se naziva kontinuirana ili integralna. Teoretski, za najbolju aproksimaciju, preporučljivo je zahtijevati da u svim tačkama određenog segmenta odstupanje aproksimirajuće funkcije od funkcije bude manje od date vrijednosti u apsolutnoj vrijednosti:,. U ovom slučaju, kaže se da funkcija ujednačeno aproksimira funkciju s preciznošću e na intervalu. Praktično dobivanje uniformne aproksimacije
2 predstavlja velike poteškoće, te se stoga ova metoda koristi uglavnom u teorijskim studijama. Najčešće korištena je takozvana aproksimacija srednjeg kvadrata, za koju vrijednost ima najmanju vrijednost. Zahtevajući da parcijalni izvod M nestane u odnosu na parametre koji određuju funkciju, dobijaju se jednadžbe koje omogućavaju pronalaženje najboljih (u navedenom smislu) vrednosti ovih parametara. Aproksimacija u kojoj je aproksimacija izgrađena na datom diskretnom skupu tačaka naziva se tačkasta aproksimacija. Da bi se dobila aproksimacija tačke srednjeg kvadrata funkcije date u tabeli, aproksimirajuća funkcija se gradi iz uslova minimuma vrednosti gde su vrednosti funkcije u tačkama. Glavno područje primjene aproksimacije srednjeg kvadrata je obrada eksperimentalnih podataka (konstrukcija empirijskih formula). Druga vrsta aproksimacije tačaka je interpolacija, u kojoj aproksimirajuća funkcija u datim tačkama uzima iste vrijednosti kao i funkcija, tj. U ovom slučaju, blizina interpolirajuće funkcije datoj funkciji je da se njihove vrijednosti poklapaju na datom sistemu bodova. Na slici su prikazani kvalitativni dijagrami interpolacijske funkcije (puna linija) i rezultati efektivne aproksimacije (isprekidana linija). Tačke označavaju tabelarne vrijednosti funkcije.,
3 INTERPOLACIJA FUNKCIJA. POSTAVKA INTERPOLACIONOG PROBLEMA Neka poznate vrijednosti neke funkcije f formiraju sljedeću tabelu: x x 0 x 1 x n f(x) y 0 y 1 y n jedna od vrijednosti x i (i=0,1,n). Klasični pristup rješavanju problema konstruiranja aproksimirajuće funkcije temelji se na zahtjevu da se vrijednosti f(x) i F(x) u tačkama x i (i=0, 1, 2, n) moraju striktno podudarati , tj. F(x 0)=y 0, F(x 1)=y 1, F(x n)=y n. (1) U ovom slučaju, pronalaženje aproksimativne funkcije naziva se interpolacija (ili interpolacija), a tačke x 0, x 1, x n su interpolacijski čvorovi. Geometrijski, to znači da morate pronaći krivu y=f(x) određenog tipa koja prolazi kroz dati sistem tačaka M i (x i, y i) (i=0,1,2,n) (vidi Sl. ). Ako je x, pronalaženje željene funkcije naziva se ekstrapolacija. U daljem tekstu termin interpolacija će označavati i prvu i drugu operaciju. Interpolacijski problem može imati nebrojen skup rješenja u općem okruženju ili ih uopće nema. Međutim, ovaj problem postaje nedvosmislen ako, umjesto proizvoljne funkcije F(x), tražimo neku funkciju specifičnog oblika koja zadovoljava uvjete (1). Najpogodnija funkcija za praktičnu upotrebu je algebarski polinom stepena n: P n (x)=a 0 x n + a 1 x n a n-1 x + a n Vrijednosti polinoma se jednostavno izračunavaju, lako ih je razlikovati, integrirati itd. Stoga su algebarski polinomi našli široku primjenu za aproksimaciju funkcija. U nastavku će biti detaljno opisani slučajevi interpolacije linearnom funkcijom (linearna interpolacija) i kvadratnom funkcijom (kvadratna interpolacija) koja se široko koristi u geografskim istraživanjima.
4 LINEARNA INTERPOLACIJA Dakle, neka nam je funkcija data u tabeli. Rješavajući interpolacijski problem, u tabeli nalazimo dvije susjedne vrijednosti argumenta (označavamo ih x k i x k + 1), između kojih se nalazi data vrijednost x (x k 5 Imajte na umu da drugi izvod funkcije f(x) ima specifično mehaničko značenje. Ako f(x) opisuje zakon kretanja materijalne tačke, onda drugi izvod ove funkcije specificira ubrzanje ove tačke u trenutku x. Činjenica postojanja ograničenja na ubrzanje (ograničenost druge derivacije) sa fizičke tačke gledišta znači da se proces opisan funkcijom f(x) odvija relativno ravnomjerno i da se funkcija ne mijenja vrlo brzo. Takva će, na primjer, biti funkcija koja s vremena na vrijeme podešava promjenu dnevne temperature zraka. U praksi, upravo ovaj kriterijum „uglađenosti“ brzine promene procesa može se u potpunosti iskoristiti za odgovor na pitanje valjanosti upotrebe linearne interpolacije. U konačnici, linearna interpolacija se smatra primjenjivom ako je dodatna greška koju unosi primjetno manja od greške mjerenja terenskih podataka. Ako sa m označimo broj posljednje znamenke vrijednosti funkcije datih u tabeli, tada će greška mjerenja biti jednaka nejednakosti: a uvjet za primjenjivost linearne interpolacije bit će napisan u obliku Međutim, dešava se da je za ispunjenje ovog uslova potrebno izabrati premali korak. U ovom slučaju ovaj uvjet se ne uzima u obzir, a za pronalaženje međuvrijednosti funkcije koriste složeniju kvadratnu interpolaciju ili druge tehnike. 6 KVADRATNA INTERPOLACIJA Neka je funkcija f(x) data u tabeli ponovo data. S obzirom da se na intervalu (x k, x k + 2) ova funkcija može zamijeniti kvadratnom funkcijom sa dovoljnim stepenom tačnosti, odnosno dio grafa funkcije može se zamijeniti parabolom (vidi sliku), Potrebno je pronaći vrijednost funkcije f (x) u nekoj tački x koja pripada intervalu (x k, x k+2). Tražit ćemo kvadratnu funkciju u sljedećem obliku: Na osnovu uslova da se vrednosti željene kvadratne funkcije poklapaju sa tabelarnim vrednostima funkcije u tri date tačke, sastavićemo sledeći sistem jednačina: Ovo je sistem od tri linearne jednadžbe sa tri nepoznate a , b i c. Njegova determinanta nije 0 (osim ako su tačke na istoj pravoj). Rešavajući sastavljeni sistem jednačina na matrični način dobijamo sledeću vezu za koeficijente, b i c: Razmotrite razliku između tačne vrijednosti funkcije f(x) i njene približne vrijednosti. Označimo ovu razliku kroz (h): (h)= f(h)-ax 2 -bx-c. 7 Došli smo do problema procjene vrijednosti funkcije j (x) za x koji prolazi kroz interval (x k, x k + 2). U slučaju koji se razmatra, moraćemo da pretpostavimo da je treći izvod funkcije f (x) na intervalu koji se razmatra kontinuiran i da zadovoljava nejednakost:. Tada vrijedi sljedeća procjena za (x): 8 REGRESIJSKA ANALIZA. POSTAVKA PROBLEMA Jedan od tipičnih zadataka obrade eksperimentalnih podataka (ED) je utvrđivanje kvantitativne zavisnosti pokazatelja kvaliteta objekta od vrijednosti njegovih parametara i karakteristika okoline. Primjer takve izjave problema je uspostavljanje veze između vremena obrade upita bazi podataka i intenziteta ulaznog toka. Vrijeme obrade ovisi o mnogim faktorima, uključujući postavljanje traženih informacija na vanjski medij, složenost zahtjeva. Stoga se vrijeme obrade za određeni zahtjev može smatrati slučajnom varijablom. Ali u isto vrijeme, sa povećanjem intenziteta toka zahtjeva, treba očekivati povećanje njegove prosječne vrijednosti, tj. uzeti u obzir da su vrijeme obrade i intenzitet toka zahtjeva u korelaciji. Izjava o problemu regresione analize je formulisana na sledeći način. Postoji skup rezultata posmatranja. U ovom skupu jedna kolona odgovara indikatoru za koji je potrebno uspostaviti funkcionalni odnos sa parametrima objekta i okruženja koje predstavljaju preostale kolone. Indikator ćemo označiti sa y * i pretpostaviti da odgovara prvoj koloni matrice posmatranja. Preostale kolone m 1 (m > 1) odgovaraju parametrima (faktorima) x 2, x 3, x m. Potrebno: uspostaviti kvantitativni odnos između indikatora i faktora. U ovom slučaju, zadatak regresione analize se podrazumijeva kao zadatak identifikacije takve funkcionalne zavisnosti y * = f (x 2, x 3, x t), koja najbolje opisuje dostupne eksperimentalne podatke. Pretpostavke: broj opservacija je dovoljan za ispoljavanje statističkih obrazaca u pogledu faktora i njihovih odnosa; obrađeni ED sadrže neke greške (šum) zbog grešaka mjerenja, utjecaja neuračunatih slučajnih faktora; matrica rezultata opservacije je jedina informacija o objektu koji se proučava koja je dostupna prije početka istraživanja. Funkcija f (x 2, x 3, x t), koja opisuje ovisnost indikatora o parametrima, naziva se regresijska jednačina (funkcija). Pojam "regresija" (regresija (lat.) povlačenje, povratak na nešto) povezuje se sa specifičnostima jednog od konkretnih zadataka koji se rješavaju u fazi formiranja metode, a trenutno ne odražava cjelokupnu suštinu metode. , ali se i dalje koristi. Rešenje problema regresione analize svrsishodno je podeliti u nekoliko faza: preliminarna obrada ED; izbor vrste regresijskih jednačina; izračunavanje koeficijenata regresione jednačine; verifikacija adekvatnosti konstruisane funkcije rezultatima posmatranja. 9 IZBOR VRSTA REGRESIJSKE JEDNAČINE Zadatak određivanja funkcionalne zavisnosti koja najbolje opisuje ED povezan je sa prevazilaženjem niza fundamentalnih poteškoća. U opštem slučaju, za standardizovane podatke, funkcionalna zavisnost indikatora od parametara može se predstaviti kao y = f(u 1, u 2,...u p) + e (1) gde f nije prethodno poznata funkcija utvrditi; e - Greška ED aproksimacije. Ova jednačina se naziva jednadžba regresije uzorka y na u. Ova jednačina karakterizira odnos između varijacije indikatora i varijacija faktora. Mjera korelacije mjeri udio varijacije indikatora koji je povezan sa varijacijom faktora. Drugim riječima, korelacija indikatora i faktora ne može se tumačiti kao odnos između njihovih nivoa, a regresiona analiza ne objašnjava ulogu faktora u kreiranju indikatora. Druga karakteristika se odnosi na procjenu stepena uticaja svakog faktora na indikator. Jednačina regresije ne daje procjenu posebnog utjecaja svakog faktora na indikator, takva procjena je moguća samo ako svi ostali faktori nisu povezani sa onim koji se proučava. Ako je proučavani faktor povezan sa drugim faktorima koji utiču na indikator, onda će se dobiti mešovita karakteristika uticaja faktora. Ova karakteristika sadrži kako direktan uticaj faktora tako i indirektan uticaj koji se vrši kroz povezanost sa drugim faktorima i njihov uticaj na indikator. Ne preporučuje se uključivanje faktora u regresionu jednačinu koji su slabo povezani sa indikatorom, ali su usko povezani sa drugim faktorima. Faktori koji su međusobno funkcionalno povezani nisu uključeni u jednačinu (za njih je koeficijent korelacije 1). Uključivanje takvih faktora dovodi do degeneracije sistema jednačina za procjenu koeficijenata regresije i do nesigurnosti rješenja. Funkcija f mora biti odabrana tako da je greška e na neki način minimalna. Postoji beskonačan skup funkcija koje opisuju ED apsolutno tačno (e = 0), tj. takve funkcije da za sve vrijednosti parametara u j,2, u j,3, u j,t uzimaju tačno odgovarajuće vrijednosti indeksa y i, i =1, 2, n. Vrijednosti indikatora mogu uzeti bilo koju vrijednost . Jasno je da takve funkcije ne odgovaraju stvarnom odnosu između parametara i indikatora. Da bi se izabrala funkcionalna veza, unaprijed se postavlja hipoteza o tome kojoj klasi funkcija f može pripadati, a zatim se bira "najbolja" funkcija u ovoj klasi. Odabrana klasa funkcija mora imati neku "glatkost", tj. "male" promjene u vrijednostima argumenata trebale bi uzrokovati "male" promjene u vrijednostima funkcije (ED sadrži neke greške mjerenja, a ponašanje samog objekta podložno je buci, maskirajući pravi odnos između parametri i indikator). Klasa polinomskih funkcija je jednostavna, zgodna za praktičnu upotrebu i ispunjava specificirani uslov (2) Za takvu klasu problem izbora funkcije se svodi na problem izbora vrednosti koeficijenata a 0, a j, a jk, a jj,. Međutim, univerzalnost polinomske reprezentacije je osigurana samo ako se stepen polinoma može neograničeno povećavati, što nije uvijek izvodljivo u praksi, pa se moraju koristiti i druge vrste funkcija. 10 Poseban slučaj koji se široko koristi u praksi je polinom prvog stepena ili jednačina linearne regresije. (3) Ovu jednačinu u regresionoj analizi treba tumačiti kao vektorsku, jer je riječ o matrici podataka, i =1, 2, n. () Obično nastoje pružiti toliki broj zapažanja koji bi premašio broj procijenjenih koeficijenata modela. Za linearnu regresiju, za n > m, broj jednačina premašuje broj polinomskih koeficijenata koji treba odrediti. Ali čak i u ovom slučaju nemoguće je odabrati koeficijente na način da greška u svakoj skalarnoj jednačini nestane, jer nepoznate uključuju a j i e i, njihov broj je n + m 1, tj. je uvijek veći od broja jednačina n. Slično razmišljanje vrijedi i za polinome višeg stepena od prvog. Za odabir vrste funkcionalne ovisnosti može se preporučiti sljedeći pristup: tačke sa vrijednostima indikatora su grafički prikazane u prostoru parametara. Sa velikim brojem parametara, moguće je izgraditi tačke za svaki od njih, dobijajući dvodimenzionalne distribucije vrednosti; po lokaciji tačaka i na osnovu analize suštine odnosa između indikatora i parametara objekta, donosi se zaključak o približnom tipu regresije ili njenim mogućim varijantama; nakon izračunavanja parametara ocjenjuje se kvalitet aproksimacije, tj. procijeniti stepen bliskosti izračunatih i stvarnih vrijednosti; ako su izračunate i stvarne vrijednosti bliske u cijelom području zadatka, tada se problem regresione analize može smatrati riješenim. U suprotnom, možete pokušati odabrati drugu vrstu polinoma ili neku drugu analitičku funkciju, kao što je periodična. 11 IZRAČUN KOEFICIJENATA REGRESIJE JEDNAČINE. METODA NAJMANJEG KVADRATA Sistem jednačina (4) na osnovu raspoloživog ED ne može se jednoznačno riješiti, jer je broj nepoznatih uvijek veći od broja jednačina. Potrebne su dodatne pretpostavke da bi se ovaj problem prevazišao. Zdrav razum sugerira da je poželjno odabrati koeficijente polinoma na način da se osigura minimalna greška u aproksimaciji ED. Za procjenu grešaka aproksimacije mogu se primijeniti različite mjere. Kao takva mjera, srednja kvadratna greška je našla široku primjenu. Na njegovoj osnovi razvijena je posebna metoda za procjenu koeficijenata regresionih jednačina, metoda najmanjih kvadrata (LSM). Ova metoda vam omogućava da dobijete procjene maksimalne vjerovatnoće nepoznatih koeficijenata regresione jednadžbe sa normalnom raspodjelom varijante, ali se može primijeniti na bilo koju drugu distribuciju faktora. LSM se zasniva na sljedećim odredbama: vrijednosti vrijednosti grešaka i faktora su nezavisne, a samim tim i nekorelirane, tj. pretpostavlja se da mehanizmi stvaranja buke nisu povezani sa mehanizmom formiranja faktorskih vrijednosti; matematičko očekivanje greške e mora biti jednako nuli (konstantna komponenta je uključena u koeficijent a 0), drugim riječima, greška je centrirana vrijednost; procjena uzorka varijanse greške treba biti minimalna. Razmotrimo primjenu najmanjih kvadrata u odnosu na linearnu regresiju standardiziranih vrijednosti. Za centrirane vrijednosti u j koeficijent a 0 je jednak nuli, zatim jednadžbe linearne regresije. (5) Ovdje se uvodi poseban znak "^" koji označava vrijednosti indikatora izračunate regresijskom jednadžbom, za razliku od vrijednosti dobijenih iz rezultata posmatranja. Prema najmanjim kvadratima određuju se takve vrijednosti koeficijenata regresijske jednadžbe koje daju bezuvjetni minimum za izraz. (6) Minimum se nalazi izjednačavanjem sa nulom svih parcijalnih izvoda izraza (6), uzetih sa nepoznatim koeficijentima, i rješavanjem sistema jednadžbi (7) Uzastopnim izvođenjem transformacija i korištenjem prethodno uvedenih procjena koeficijenata korelacije 12 dobijamo. (8) Tako su dobijene m 1 linearne jednadžbe koje omogućavaju jedinstveno izračunavanje vrijednosti a 2, a 3, a m. Upotreba LSM-a za nelinearne funkcije praktično se ne razlikuje od razmatrane šeme (samo koeficijent a 0 u originalnoj jednačini nije jednak nuli). Na primjer, neka je potrebno odrediti koeficijente paraboličke regresije = a 0 + a 2 u 2 + a 22 u 2 2. Varijanca greške uzorka. Na osnovu njega možete dobiti sledeći sistem jednačina.Nakon transformacija sistem jednačina će poprimiti oblik Uzimajući u obzir svojstva momenata standardizovanih veličina, pišemo Definicija koeficijenata nelinearne regresije zasnovana je na rešavanju sistema linearnih jednačina. Da biste to učinili, možete koristiti univerzalne pakete numeričkih metoda ili specijalizirane pakete za obradu statističkih podataka. Kako se stepen regresione jednačine povećava, povećava se i stepen momenata distribucije parametara koji se koriste za određivanje koeficijenata. Da, za 13 za određivanje koeficijenata regresione jednačine drugog stepena koriste se momenti distribucije parametara do zaključno četvrtog stepena. Poznato je da tačnost i pouzdanost procene momenata iz ograničenog uzorka DE naglo opada sa povećanjem reda. Upotreba polinoma stepena višeg od drugog u regresijskim jednačinama nije preporučljiva. Kvalitet rezultirajuće jednačine regresije se ocjenjuje stepenom bliskosti između rezultata posmatranja indikatora i vrijednosti predviđenih regresionom jednadžbom u datim tačkama u prostoru parametara. Ako su rezultati bliski, onda se problem regresione analize može smatrati riješenim. U suprotnom, trebali biste promijeniti jednadžbu regresije (odabrati drugi stepen polinoma ili potpuno drugu vrstu jednačine) i ponoviti proračune da biste procijenili parametre. Ako postoji više indikatora, problem regresione analize rješava se nezavisno za svaki od njih. Analizirajući suštinu regresione jednačine, treba napomenuti sljedeće odredbe. Razmatrani pristup ne daje odvojenu (nezavisnu) ocjenu koeficijenata. Promjena vrijednosti jednog koeficijenta povlači promjenu vrijednosti drugih. Dobijene koeficijente ne treba smatrati doprinosom odgovarajućeg parametra vrijednosti indikatora. Jednačina regresije je samo dobar analitički opis dostupnog ED, a ne zakon koji opisuje odnos između parametara i indikatora. Ova jednadžba se koristi za izračunavanje vrijednosti indikatora u datom rasponu promjena parametara. Postavljanje problema, osnovni pojmovi Konačne razlike i njihova svojstva Interpolacijski polinomi Procjena preostalog člana interpolacijskih polinoma Postavka problema, osnovni pojmovi Neka, tj. Kremenčug Nacionalni univerzitet nazvan po Mihailu Ostrogradskom MATEMATIČKE METODE MODELIRANJA Matematičke metode računarskih proračuna Cherny, doktor tehničkih nauka, profesor http:\\saue.kdu.edu.ua 2 PREDAVANJE METODE INTERPOLACIJE I APROKSIMACIJE APOKSIMACIJA FUNKCIJA NUMERIČKA DIFERENCIJACIJA I INTEGRACIJA U ovom odeljku razmatramo probleme aproksimacije funkcija korišćenjem Lagranžovih i Njutnovih polinoma korišćenjem splajn interpolacije 66 Dakle, tačka A je globalna tačka maksimuma, a tačka M globalna minimalna tačka date funkcije u zatvorenom području D 5 Empirijske formule Određivanje parametara empirijskih formula 1 Lagrangeov polinom Neka se iz eksperimenta dobiju vrijednosti nepoznate funkcije (x i = 01 x [ a b] i i i). Konstrukcija MM statike tehnoloških objekata Prilikom proučavanja statike tehnoloških objekata najčešće se susreću objekti sa sledećim tipovima blok dijagrama (sl. O sa jednim ulazom x i jednim Postavka aproksimacionog problema Linearna, nelinearna (drugog reda) aproksimacija Predavanje 5 Postavljanje aproksimacionog problema Neka, proučavajući nepoznatu funkcionalnu zavisnost y=f(x), Predavanje 3 5. METODE APOKSIMACIJE FUNKCIJA FORMULACIJA ZADATAKA Razmatraju se funkcije tabele mreže [ a b] y 5 definisane u čvorovima mreže Ω. Svaka mreža je karakterizirana koracima h neujednačenosti ili h Predmet. Numeričke metode za rješavanje problema aproksimacije Pretpostavljamo da je to funkcija argumenta. To znači da je bilo kojoj vrijednosti u opsegu dodijeljena vrijednost. Na praksi PREDAVANJE 3 Metode obrade eksperimentalnih podataka Interpolacija Stranica Interpolacija - promjena (lat.) Aproksimacija - aproksimacija (lat.) Interpolacija mrežnih funkcija Predavanje 4. Rješavanje sistema linearnih jednačina jednostavnim iteracijama. Ako sistem ima veliku dimenziju (6 jednačina) ili je matrica sistema rijetka, indirektne iterativne metode su efikasnije za rješavanje. MINISTARSTVO OBRAZOVANJA I NAUKE Ruske Federacije R.E. Numeričke metode Tema 2 Interpolacija V I Velikodny 2011 2012 akademska godina 1 Koncept interpolacije Interpolacija je metoda aproksimativnog ili tačnog pronalaženja bilo koje veličine iz poznatih pojedinačnih vrijednosti Ojlerova metoda Zadatak pronalaženja određenog rješenja diferencijalne jednadžbe () f (6.) može se približno riješiti numeričkim metodama. Za pronalaženje određenog rješenja jednačine (6.) na segmentu [ a Laboratorijski rad Interpolacija i aproksimacija funkcija Svrha rada je proučavanje polinomskih funkcija, interpolacijskih metoda u programskom paketu Matlab. Sadržaj: 1. Predstavljanje polinoma i računanje 46 Poglavlje 9. Regresiona analiza 9.. Zadaci regresione analize Prilikom statističkih posmatranja, po pravilu se dobijaju vrijednosti nekoliko karakteristika. Radi jednostavnosti, dalje ćemo razmatrati dvodimenzionalno MINISTARSTVO OBRAZOVANJA RUJSKE FEDERACIJE Državna obrazovna ustanova visokog stručnog obrazovanja "Iževski državni tehnički univerzitet" ODOBRIO rektor I.V. Abramov Golubev VO Litvinova TE Implementacija algoritma za konstruisanje statističkog modela objekta korišćenjem Brandonove metode Postavljanje problema Statistički modeli se kreiraju na osnovu dostupnih eksperimentalnih podataka 6. Traženje empirijskih formula. Aproksimacija 6 .. Koncept regresije i korelacije Prilikom proučavanja različitih pojava potrebno je pozabaviti se funkcionalnim odnosima između dvije ili više varijabli. Kada ovi Zavisnost od linearne korelacije Često je u praksi potrebno utvrditi oblik i procijeniti jačinu ovisnosti slučajne varijable Y koja se proučava od jedne ili više drugih varijabli (slučajnih ili neslučajnih). PREDAVANJA IZ RAČUNSKE MATEMATIKE ES Tverskaya MSTU im. N.E. Bauman Moskva Metode aproksimacije funkcije. Izjava o problemu aproksimacije funkcije. Problemi koji dovode do problema aproksimacije funkcija. Funkcija Predavanje nastavak predavanja METODE INTEGRALNOG GLAĐIVANJA TAČKE METODA NAJMANJIH KVADRATA Laboratorijski rad 6. Konstrukcija empirijske zavisnosti toplotnog kapaciteta supstance od temperature. Koncept statističke zavisnosti Dvije veličine (na primjer, x i y) mogu biti nezavisne ili povezane 3 Interpolacija funkcija Lagrangeovim polinomom Svrha: formiranje vještina interpolacije tabelarno datih funkcija Lagrangeovim polinomom; procjena greške za Lagrangeov polinom Kratke teoretske informacije 6 Metode aproksimacije funkcija. Najbolja aproksimacija. Metode aproksimacije koje se razmatraju u prošlom poglavlju zahtijevaju da čvorovi mrežne funkcije striktno pripadaju rezultujućem interpolantu. Ako nije potrebno 3. Interpolacija podataka 1 3. Interpolacija podataka Gotovo uvijek, uzorci slučajnih brojeva (dobijeni kao rezultat eksperimenta ili generirani primjenom Monte Carlo metoda) se pohranjuju na računarima Predavanje 5. Elementi teorije korelacije Funkcionalna, statistička i korelaciona zavisnost. Dvije slučajne varijable se mogu povezati funkcionalnom zavisnošću, tj. menjanje jednog od njih PREDAVANJE 7 INTERPOLACIJA Na prošlom predavanju razmatran je problem rješavanja predeterminiranog sistema. Takav sistem ima oblik: a 11 x 1 + a 1 x + + a 1 x = f 1, ( a 1 x 1 + a x + + a x = f, ( a 1 x 1 + a x Regresiona analiza [Deo II, str. 59-68] Regresiona analiza je dizajnirana za dobijanje teorijske regresione jednačine = f(,), čiji se oblik postavlja na osnovu karakteristika sistema slučajnih varijabli koji se proučava. JEDNOFABRIČKA REGRESIJSKA ANALIZA Svrha rada je izvođenje jednosmjerne regresione analize zasnovane na polinomskim modelima prvog, drugog i trećeg reda. Teorijska osnova. pod regresijom Matematičko modeliranje termoenergetskih objekata Predavanje 1. Nelinearne algebarske i transcendentalne jednadžbe. Termini i koncepti 2 Modeliranje je proučavanje objekta ili sistema objekata pomoću Predavanje 0.3. Koeficijent korelacije U ekonometrijskoj studiji, pitanje prisustva ili odsustva veze između analiziranih varijabli rješava se metodama korelacione analize. Samo INTERPOLACIJA FUNKCIJA NAVEDBA ZADATAKA Date su: tačke posmatranja y (njihov broj +) a b ; ; y y y y Funkcija pronalaženja: F F: y Definicija Tačke y se nazivaju interpolacijski čvorovi Grafička interpretacija LSM aproksimacija Izglađivanje eksperimentalnih zavisnosti metodom najmanjih kvadrata (aproksimacija) Jedan od glavnih zadataka matematičke statistike je pronalaženje zakona distribucije slučajnih NUMERIČKE METODE U RUDARSKOJ INDUSTRIJI Matematički modeli i numeričke metode Aproksimacija tabelarno definisanih funkcija Tabelarni definisane funkcije. Zavisnost napona pražnjenja plinske praznine sa jednoličnim poljem od udaljenosti između elektroda Udaljenost između kuglica, cm Prečnik MVDubatov Teorija verovatnoće i matematička statistika Predavanje 4 Regresiona analiza Funkcionalne statističke i korelacione zavisnosti U mnogim primenjenim (uključujući ekonomske) problemima 3.4. STATISTIČKE KARAKTERISTIKE ODABRANIH VRIJEDNOSTI MODELA PREDVIĐANJA Do sada smo razmatrali metode za konstruisanje prediktivnih modela stacionarnih procesa, ne uzimajući u obzir jednu veoma važnu osobinu. Ministarstvo obrazovanja i nauke Ruske Federacije Federalna državna budžetska obrazovna ustanova visokog stručnog obrazovanja "Moskovski državni tehnički univerzitet" APOKSIMACIJA TABELINIH FUNKCIJA METODOM najmanjeg kvadrata Izjava aproksimacionog problema Na osnovu rezultata eksperimenata dobija se tabela sa proizvoljnim rasporedom argumenata: x, y. Analitički MINISTARSTVO OBRAZOVANJA I NAUKE RUJSKE FEDERACIJE Moskovski državni univerzitet za geodeziju i kartografiju (MIIGAiK) Fakultet za učenje na daljinu 5 Metode aproksimacije funkcija. Interpolacija tabličnih funkcija. 5.1 Izjava o problemu aproksimacije funkcija. Aproksimacija funkcija se sastoji u približnoj zamjeni date funkcije f(x nekom funkcijom Kremenčug Nacionalni univerzitet nazvan po Mihailu Ostrogradskom MATEMATIČKE METODE MODELIRANJA Matematičke metode računarskih proračuna Black, doktor tehničkih nauka, profesor http:\\sue.kdu.edu.u 2 PREDAVANJE 55 3 REGRESIJSKA ANALIZA 3 Izjava o problemu regresione analize Ekonomski pokazatelji funkcionisanja preduzeća (sektora privrede) obično su predstavljeni tabelama statističkih podataka: MOSKVSKI DRŽAVNI TEHNIČKI UNIVERZITET nazvan po N.E. BAUMANA SP Erkovich PRIMENA REGRESIJE I KORELACIONE ANALIZE ZA PROUČAVANJE ZAVISNOSTI U FIZIČKOJ PRAKSI. Moskva, 994. Tema 2.3. Izgradnja linearnog regresijskog modela ekonomskog procesa Neka postoje dvije mjerene slučajne varijable (CV) X i Y. Kao rezultat n mjerenja, dobijeno je n nezavisnih parova. Prije APROKSIMACIJA U praksi se često susrećemo sa problemom izglađivanja eksperimentalnih podataka, problemom aproksimacije. Glavni zadatak aproksimacije je konstrukcija aproksimativne (aproksimativne) funkcije INTERPOLACIJA TABELENIH ZAVISNOSTI PO POLINOMA U OKRUŽENJU ET MS EXCEL I MATEMATIČKI PAKET MATHCAD Aleshin A. O., Rasteryaev N.V. Donski državni tehnički univerzitet (DSTU) Rostov na Donu, RAČUNSKI I GRAFIČKI RAD 4 Interpolacija tabelarnih podataka. Kratke teorijske informacije Predavanje 8 Tema Poređenje slučajnih varijabli ili karakteristika. Sadržaj teme Analogija diskretnih SV i uzoraka Tipovi zavisnosti dve slučajne varijable (uzorci) Funkcionalna zavisnost. regresijske linije. Ministarstvo prosvete i nauke Ruske Federacije MOSKVSKI DRŽAVNI UNIVERZITET ZA GEODEZIJU I KARTOGRAFIJU (MIIGAiK) Fakultet za učenje na daljinu 0 7 APOKSIMACIJA EKSPERIMENTALNIH PODATAKA METODOM najmanjeg kvadrata U početku se podaci istraživanja prikazuju u obliku tabela. Međutim, tabelarni podaci nisu vizualni i ne mogu se koristiti Poglavlje 4 Sistemi linearnih jednadžbi Predavanje 7 Opća svojstva Definicija Normalni sistem (NS) linearnih diferencijalnih jednadžbi je sistem oblika x A () x + F () () gdje je A() kvadratna matrica Tema 4. NUMERIČKO RJEŠENJE NELINEARNIH JEDNAČINA -1- Tema 4. NUMERIČKO RJEŠENJE NELINEARNIH JEDNAČINA 4.0. Izjava problema Problem pronalaženja korijena nelinearne jednadžbe oblika y=f() često se susreće u znanstvenim Izbor vrste i određivanje parametara empirijske zavisnosti Metodološka uputstva za teorijski deo. empirijski pristup. Često se prije istraživanja u bilo kojoj oblasti javlja sljedeći problem. Dostupan Predavanje 5. Aproksimacija funkcija metodom najmanjih kvadrata. U inženjerskim djelatnostima često postaje potrebno opisati u obliku funkcionalnog odnosa odnos između vrijednosti datih u tabeli. Laboratorijski rad 6. Aproksimacija funkcija Aproksimacija (aproksimacija) funkcije f (x) je nalaženje takve funkcije g (x) (aproksimirajuća funkcija), koja bi bila bliska datoj. Kriterijumi "Optimizacija i matematičke metode odlučivanja" čl. nastavnik cafe SS i PD Sergej Aleksandrovič Vladimirov Predavanje 4 Metode matematičke statistike u problemima odlučivanja Uvod SADRŽAJ INTERPOLACIJA POLINOMAMA Uvod Naučnici i inženjeri se često moraju baviti funkcijama definisanim u tabeli. Funkcije ove vrste nastaju kada se radi sa eksperimentalnim, statističkim Poglavlje 7 Obrada eksperimentalnih rezultata u OpeOffice.org Calc U ovom poglavlju ćemo istražiti mogućnosti OpeOffice.org Calc paketa za rešavanje problema obrade eksperimentalnih podataka. Jedan od uobičajenih METODA NAJMANJEG KVADRATA (LSM) 1. Dozvolite da proučavate zavisnost jedne fizičke veličine y od druge x, odnosno potražite zavisnost y (x). Na primjer, to može biti ovisnost gustine tvari o temperaturi Laboratorijski rad 5. Linearna i kvadratna interpolacija. Izjava o problemu aproksimacije funkcija. Iskaz problema: potrebno je približno zamijeniti (aproksimirati) datu funkciju f(x) nekim 9.5.4. NUMERIČKA INTEGRACIJA DIFERENCIJALNIH JEDNAČINA PRVOG REDA Varijanta na intervalu [ ; ] sa korakom po Ojlerovoj metodi, modifikovanoj Eulerovoj metodi i Runge-Kutta metodi. pronaći tačno rješenje i 7. KORELACIONA-REGRESIJA ANALIZA Linearna regresija Najmanji kvadrati () Linearna korelacija () () 1 Vježba 7 KORELACIONA-REGRESIJA ANALIZA Za rješavanje praktičnih Lekcija 3 REGRESIJSKA ANALIZA ZA OBRADU EKSPERIMENTALNIH REZULTATA Regresiona analiza se često koristi u hemiji za obradu eksperimentalnih podataka, čiju ukupnost predstavljaju neki RJEŠENJE NELINEARNIH JEDNAČINA I SISTEMA NELINEARNIH JEDNAČINA.. RJEŠENJE NELINEARNIH JEDNAČINA oblika Numeričko rješenje nelinearnih algebarskih ili transcendentalnih jednačina. je pronaći vrijednosti Metoda iteracije Neka je data jednadžba s jednom nepoznatom ((5) Metodom pronalaženja približnih vrijednosti korijena jednadžbe (5 pomoću formule MINISTARSTVO OBRAZOVANJA I NAUKE RUSKOG FEDERALNOG DRŽAVNOG BUDŽETA OBRAZOVNA USTANOVA VISOKOG OBRAZOVANJA "VORONJEŽ DRŽAVNI UNIVERZITET" FILIJALA BORISOGLEB (BF FGBOU VO "VSU") ODOBRILA Rukovodioca 0 Evaluacija bliskosti bilo koje korelacije Bliskost linearne korelacije je razmatrana gore. Kako procijeniti bliskost bilo koje korelacije? Neka se sumiraju podaci opservacije o karakteristikama X i Y